A1 Tonerzeugung E-Gitarre

Die E-Gitarre ist eines der wichtigsten Instrumente in der Pop- und Rockmusik. Der Tonabnehmer einer E-Gitarre besteht aus einer Spule und sechs darin steckenden zylinderförmigen Magneten. Jede der Gitarrensaiten befindet sich genau über „ihrem“ Magneten. Durch die Schwingung der Saite wird im Tonabnehmer eine Spannung induziert, die dann über einen Verstärker in ein akustisches Signal umgewandelt wird.

Rote E‑Gitarre mit Hals, Tonabnehmern und sechs Saiten

Die Funktionsweise eines Tonabnehmers einer E-Gitarre soll im Folgenden mit einem vereinfachten Modell untersucht werden.

Stelle in Material 1 Abb. 1 die Struktur des Magnetfelds durch Feldlinien dar.

3 BE

Erkläre mithilfe von Material 2 Abb. 2, dass durch die Schwingung der Blattfeder eine Wechselspannung in der Spule des Tonabnehmer-Modells induziert wird, die die gleiche Frequenz aufweist wie die Schwingung.

4 BE

Erläutere jeweils mithilfe von Material 2 Abb. 2 qualitativ den Einfluss der folgenden Größen auf den maximal auftretenden Betrag der Induktionsspannung an der Spule:

Schwingungsamplitude der Blattfeder bei gleichbleibender Frequenz
Abstand zwischen Blattfeder und Spule in der Ruhelage bei gleicher Auslenkung der Blattfeder

3 BE

Die beiden Umkehrpunkte der Schwingung werden mit Formula: P_1 bzw. Formula: P_2 bezeichnet, wobei der Umkehrpunkt ist, der weiter von der Spule entfernt liegt (vgl. Material 2 Abb. 2). Ordne den Umkehrpunkten und begründet jeweils einen der Messpunkte Formula: A, B, C oder Formula: D in Material 2 Abb. 3 zu.

4 BE

Bei einer Gitarre ist die Schwingungsfrequenz indirekt proportional zur Länge des schwingenden Teils der Saite. Mit dem Versuchsaufbau aus Material 2 Abb. 2 soll nun untersucht werden, ob dies auch für die Blattfeder gilt.

Ermittle mithilfe von Material 2 Abb. 3 die Frequenz möglichst genau, die sich für $Formula: L = 15\;\text{cm}$ $Formula: L = 15\;\text{cm}$ ergibt. Erläutere das Vorgehen, um einen möglichst genauen Wert zu erhalten.

4 BE

Überprüfe mithilfe der Werte aus Material 3 und einer geeigneten grafischen Darstellung, ob auch für die Blattfeder die indirekte Proportionalität zwischen der Frequenz Formula: f und der Länge Formula: L des schwingenden Teils der Blattfeder gilt. Berücksichtige dabei die angegebenen Messunsicherheiten.

5 BE

Erkläre schrittweise und logisch klar gegliedert die Veränderung der Frequenz der Induktionsspannung und des maximal auftretenden Betrages der Induktionsspannung mit zunehmender Länge Formula: L des schwingenden Teils der Blattfeder. Gehe dabei von jeweils gleicher Auslenkung zu Beginn der Messung und gleichem Abstand Formula: d zwischen Blattfeder und Spule in der Ruhelage aus.

4 BE

In einem Internetforum wird behauptet, dass die Amplitude der Induktionsspannung größer wird, wenn der Dauermagnet im Modellversuch nicht am Eisenkern, sondern an der Blattfeder befestigt wird. Damit könne auch auf den Eisenkern verzichtet werden.

Zur Überprüfung dieser Behauptung soll eine Abschätzung des maximalen Betrages der Induktionsspannung $Formula: U_\text{max}$ $Formula: U_\text{max}$ mit einem entsprechend veränderten Modellversuch (siehe Material 4 Abb. 4) vorgenommen werden.

Markiere in Material 4 Abb. 5 einen Zeitpunkt, an dem die zeitliche Änderung des Betrags der magnetischen Flussdichte $Formula: \dot{B}$ $Formula: \dot{B}$ ihren maximalen Wert $Formula: \dot{B}_{\text{max}}$ $Formula: \dot{B}_{\text{max}}$ annimmt.

Ermittle an dieser Stelle einen Wert für $Formula: \dot{B}_{\text{max}}$ $Formula: \dot{B}_{\text{max}}$ und damit unter Verwendung des Induktionsgesetzes einen Wert für $Formula: U_\text{max}$ $Formula: U_\text{max}$ für die in Material 4 beschriebene Spule.

8 BE

Bei der Durchführung des Experiments aus Material 4 Abb. 4 ergibt sich für $Formula: U_\text{max}$ $Formula: U_\text{max}$ ein Wert von $Formula: 0,04\;\text{V},$ $Formula: 0,04\;\text{V},$ im Vergleich zu $Formula: 0,11\;\text{V}$ $Formula: 0,11\;\text{V}$ mit dem Versuchsaufbau aus Material 2 Abb. 2. Damit ist die Behauptung aus dem Internetforum widerlegt.

Gib einen Grund für die Abweichung des in Teilaufgabe 2a berechneten Werts vom gemessenen Wert an.

2 BE

Beurteile aus Sicht eines Gitarrenspielers anhand eines Arguments, ob die Bauweise analog zu Material 4 Abb. 4 für eine E-Gitarre sinnvoll ist.

2 BE

40 BE

Material 1: Modell für den Tonabnehmer

Das Modell für den Tonabnehmer besteht aus einer Spule mit Eisenkern, der durch einen Permanentmagneten magnetisiert wird (siehe Abb. 1).

Abb. 1: Basis des Tonabnehmer-Modells

Material 2: Modell für den Tonabnehmer mit schwingender Saite

Die Tonhöhe einer Gitarrensaite wird durch die Länge ihres schwingungsfähigen Teils beeinflusst. Im Modell repräsentiert eine schwingende Blattfeder aus Eisen die Gitarrensaite.

Abb. 2 zeigt, von oben betrachtet, den auf dem Experimentiertisch liegenden Versuchsaufbau. Die Blattfeder schwingt parallel zur Oberfläche des Experimentiertisches, weswegen der Einfluss der Gewichtskraft vernachlässigt werden kann.

Die verschiebbare Halterung gewährleistet, dass sich das Ende der Blattfeder unabhängig von der jeweiligen Länge Formula: L des schwingenden Teils der Blattfeder stets genau auf Höhe des Eisenkerns befindet (siehe Abb. 2).

Abb. 2

Wird die Blattfeder ausgelenkt, so ergibt sich für $Formula: L = 15,0\;\text{cm}$ $Formula: L = 15,0\;\text{cm}$ der in Abb. 3 dargestellte Verlauf für die Induktionsspannung. Dabei ist $Formula: U_\text{max}$ $Formula: U_\text{max}$ der maximal auftretende Betrag der Spannung.

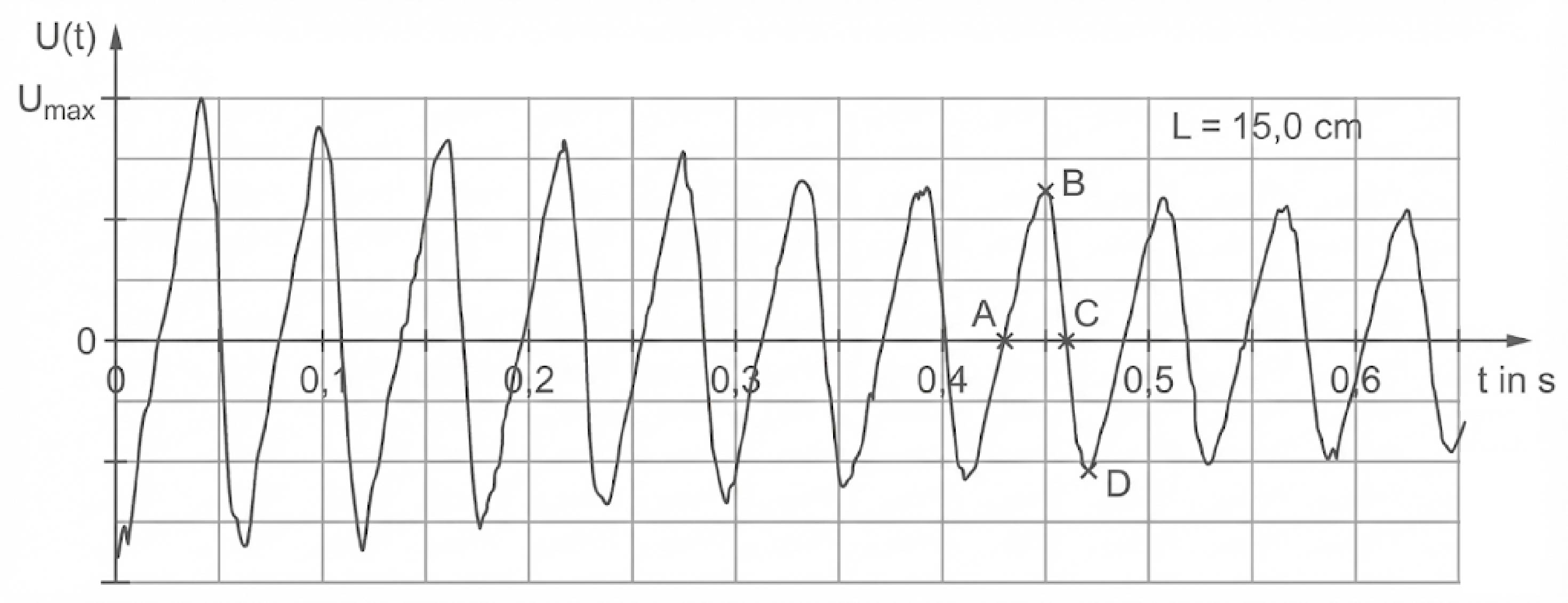
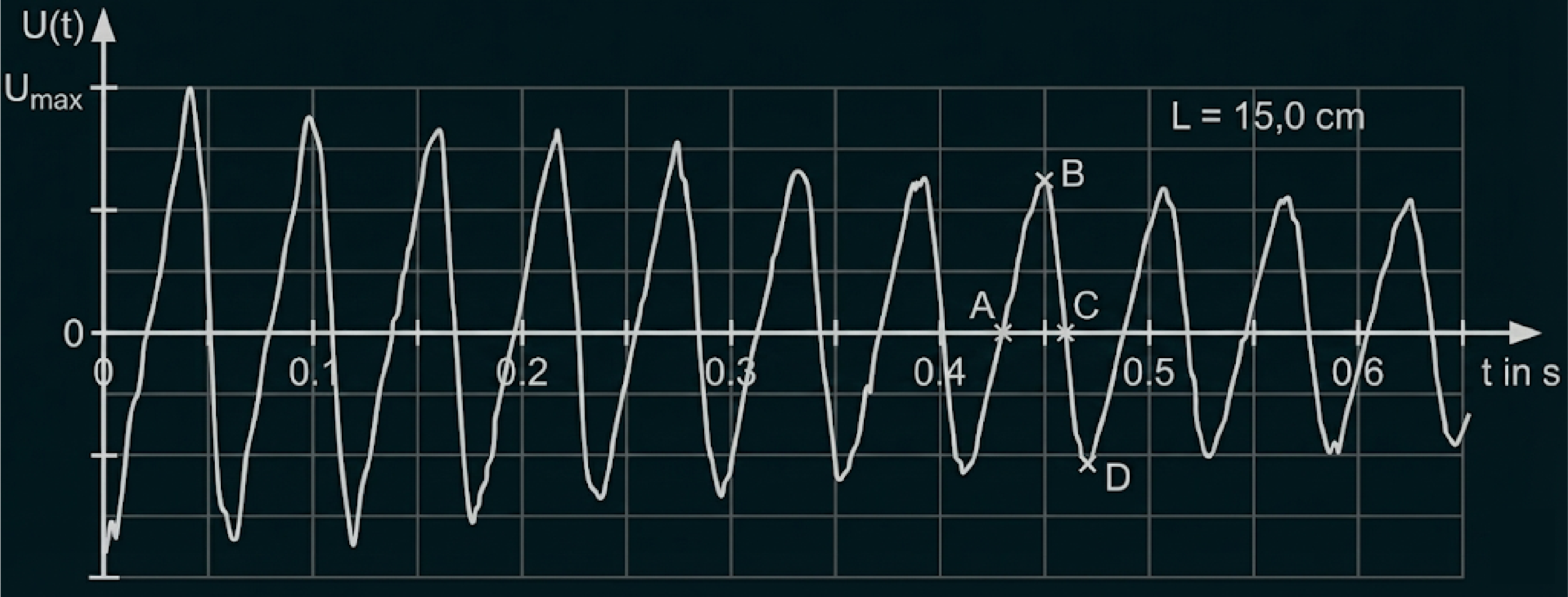
U(t)-Diagramm mit mehreren Schwingungen von 0 bis 0,6 s, Gitterlinien und markierten Punkten A, B, C, D.

Abb. 3

Material 3: Frequenz in Abhängigkeit von der Länge

In Messreihen mit weiteren Längen Formula: L des schwingenden Teils der Blattfeder sind unter sonst gleichen Bedingungen folgende Frequenzen Formula: f mit ihren jeweiligen Unsicherheiten ermittelt worden:

$Formula: \boldsymbol{L}$ $Formula: \boldsymbol{L}$ in cm	$Formula: \boldsymbol{f}$ $Formula: \boldsymbol{f}$ in Hz
	$Formula: 40,4 \pm 4,0$ $Formula: 40,4 \pm 4,0$
	$Formula: 10,0 \pm 0,3$ $Formula: 10,0 \pm 0,3$
	$Formula: 6,5 \pm 0,1$ $Formula: 6,5 \pm 0,1$

Material 4: Schwingender Magnet

Abb. 4 zeigt, von oben betrachtet, den veränderten Versuchsaufbau (Spule: Formula: N = 1000; $Formula: A = 16\;\text{cm}^2$ $Formula: A = 16\;\text{cm}^2$ ).

Abb. 4

Unter der Annahme, dass die Blattfeder $Formula: (L = 15,0\;\text{cm})$ $Formula: (L = 15,0\;\text{cm})$ mit dem darauf befestigten Magneten harmonisch schwingt, und unter Vernachlässigung von Einflüssen durch die Spule ergibt sich für den Betrag Formula: B der magnetischen Flussdichte im Punkt Formula: Q (vgl. Abb. 4) ein zeitlicher Verlauf, wie er in Abb. 5 dargestellt ist.

Zeitlicher Verlauf der magnetischen Flussdichte

Abb. 5

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Feldlinienbild eines Magnetfelds eines Tonabnehmers

Die Blattfeder befindet sich im Magnetfeld des durch den Permanentmagneten magnetisierten Eisenkerns (vgl. Teilaufgabe a). Da die Blattfeder aus Eisen ist, wird sie ebenfalls magnetisiert. Schwingt sie nach links und rechts, ändert sich durch den veränderten Abstand der magnetische Fluss in der Spule. Folglich wird nach dem Induktionsgesetz eine Spannung zwischen den beiden Spulenenden induziert. Da die Abstandsänderung periodisch mit der Frequenz der Federschwingung erfolgt, besitzt auch die induzierte Spannung diese Frequenz.

Die größere Amplitude der Federschwingung bewirkt eine in gleichen Zeiteinheiten (gleiche Frequenz!) größere Änderung der magnetischen Flussdichte und damit nach dem Induktionsgesetz eine größere Amplitude der induzierten Wechselspannung.
Das magnetische Feld der Spule wird mit zunehmendem Abstand schwächer. Befindet sich die Feder daher weiter entfernt von der von der Spule und schwingt dabei mit unveränderter Auslenkung, ist die magnetische Flussdichte und damit auch ihre durch die schwingende Blattfeder verursachte Änderung kleiner als nahe der Spule. Folglich wird nach dem Induktionsgesetz mit zunehmendem Abstand die Amplitude der Induktionsspannung kleiner.

An den Umkehrpunkten der Federschwingung wechselt die Bewegungsrichtung. Somit ist dort die Geschwindigkeit der Feder null, es findet folglich keine Flussänderung statt und die induzierte Spannung ist null. Damit kommen für die Punkte Formula: P_1 und Formula: P_2 nur die Nullstellen Formula: A und Formula: C in Frage. Bei wird die Spannung positiv, also nimmt nach dem Induktionsgesetz der magnetische Fluss ab. Diese Abnahme kann nur auf dem Weg der Feder von nach erfolgen, weil sich längs dieses Weges der Abstand zur Spule vergrößert; entspricht also der Nullstelle Formula: A. Die Feder bewegt sich nach Verlassen des Umkehrpunkts schneller und beim Durchgang durch die Ruhelage mit maximaler Geschwindigkeit (entspricht dem Spannungsmaximum bei Formula: B ). Dann wird sie wieder langsamer bis zum Umkehrpunkt Formula: P_1, der folglich der Nullstelle Formula: C entspricht.

Die Frequenz Formula: f lässt sich aus der Schwingungsdauer Formula: T über $Formula: f=\tfrac{1}{T}$ $Formula: f=\tfrac{1}{T}$ berechnen. Im Bereich von $Formula: 0,10\;\mathrm{s}$ $Formula: 0,10\;\mathrm{s}$ bis $Formula: 0,45\;\mathrm{s}$ $Formula: 0,45\;\mathrm{s}$ finden genau Formula: 6 Schwingungen statt, also ist die Schwingungsdauer

$Formula: T=\dfrac{0,45\;\mathrm{s}-0,10\;\mathrm{s}}{6}=\dfrac{0,35\;\mathrm{s}}{6}=0,058\;\mathrm{s}$ $Formula: T=\dfrac{0,45\;\mathrm{s}-0,10\;\mathrm{s}}{6}=\dfrac{0,35\;\mathrm{s}}{6}=0,058\;\mathrm{s}$

und die Blattfederfrequenz beträgt somit

$Formula: f=\dfrac{1}{0,058\;\mathrm{s}}=17\;\mathrm{Hz}$ $Formula: f=\dfrac{1}{0,058\;\mathrm{s}}=17\;\mathrm{Hz}$

Erläuterung des Vorgehens

Der Messfehler beim Ablesen ist unabhängig davon, ob eine oder mehrere Perioden abgelesen werden, gleich groß. Daher verbessert sich die Messgenauigkeit, wenn die Dauer Formula: t mehrerer Perioden (hier

$Formula: t=0,35\;\mathrm{s}$ $Formula: t=0,35\;\mathrm{s}$ für Formula: n=6 ) abgelesen wird und dann mittels Division $Formula: \tfrac{t}{n}$ $Formula: \tfrac{t}{n}$ bestimmt wird. Der konstante Ablesefehler wird dann ebenfalls durch geteilt. Im Beispiel hier beträgt er dann nur noch ein Sechstel im Vergleich zum Ablesen einer einzigen Periodenzeit (absoluter Fehler gleich, relativer Fehler kleiner).

Um zu prüfen, ob Blattfederlänge Formula: L und Frequenz Formula: f zueinander umgekehrt proportional sind (wie bei der Gitarrensaite), könnte geprüft werden, ob die Werte auf einer geeigneten Hyperbel liegen. Genauer und einfacher ist es, die (direkte!) Proportionalität zwischen $Formula: \tfrac{1}{L}$ $Formula: \tfrac{1}{L}$ und zu prüfen, die Werte müssen dann auf einer Ausgleichsgeraden liegen.

Ergänzen der Tabelle um $Formula: \tfrac{1}{L}$ $Formula: \tfrac{1}{L}$ liefert:

$Formula: \boldsymbol{L}$ $Formula: \boldsymbol{L}$ in cm	$Formula: \boldsymbol{\tfrac{1}{L}}$ $Formula: \boldsymbol{\tfrac{1}{L}}$ in $Formula: \boldsymbol{\tfrac{1}{\text{m}}}$ $Formula: \boldsymbol{\tfrac{1}{\text{m}}}$	$Formula: \boldsymbol{f}$ $Formula: \boldsymbol{f}$ in Hz
		$Formula: 40,4 \pm 4,0$ $Formula: 40,4 \pm 4,0$
		$Formula: 10,0 \pm 0,3$ $Formula: 10,0 \pm 0,3$
		$Formula: 6,5 \pm 0,1$ $Formula: 6,5 \pm 0,1$

Einzeichnen der Wertepaare $Formula: \left( \left.\dfrac{1}{L}\,\right\vert\, f\right)$ $Formula: \left( \left.\dfrac{1}{L}\,\right\vert\, f\right)$ einschließlich der Fehlerbalken für Formula: f in ein Diagramm und überprüfen, ob sie auf einer Ursprungsgeraden liegen, liefert:

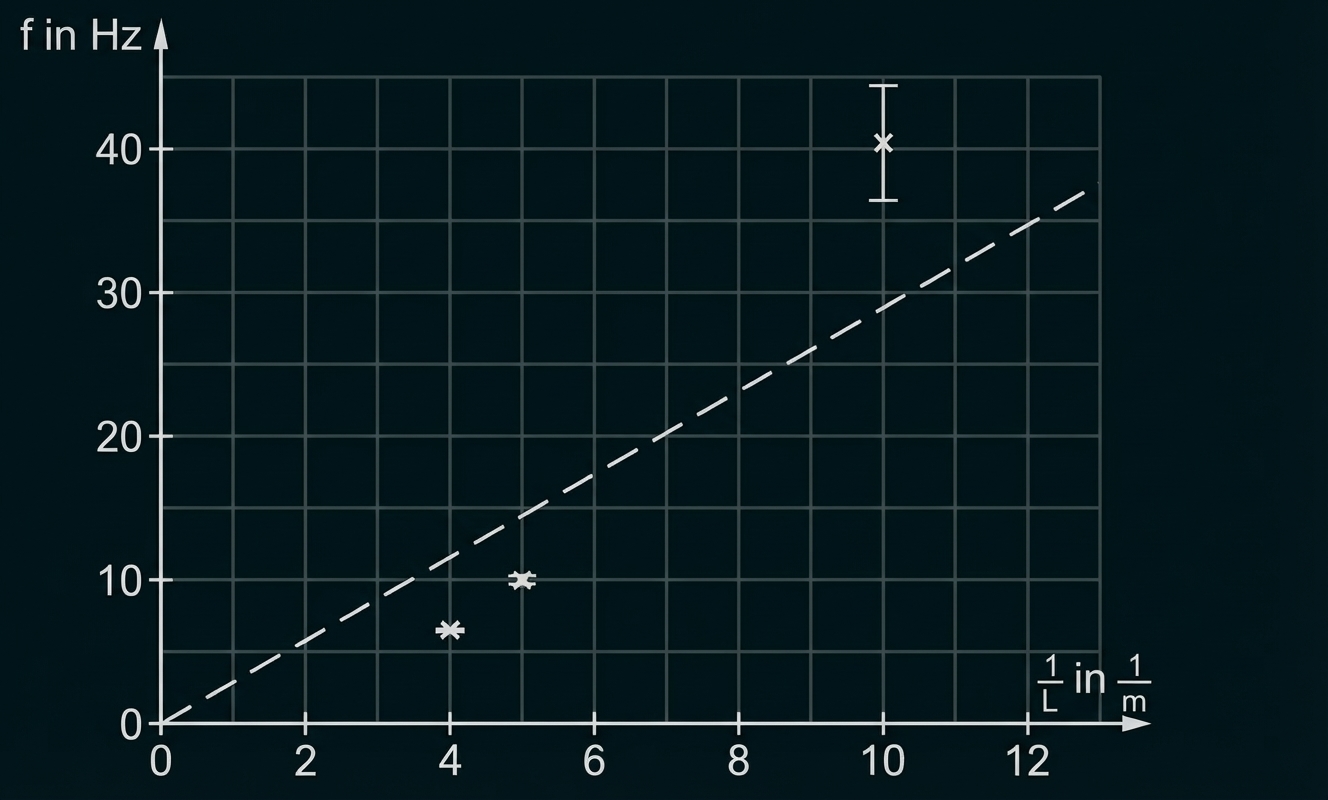
Überprüfen der direkten Proportionalität mit Ursprungsgeraden

Das ist nicht der Fall: Eine geeignete Ausgleichsgerade lässt sich nicht einmal im Fehlerbereich einzeichnen. Folglich kann zwischen Formula: L und Formula: f keine indirekte Proportionalität bestehen.

Frequenz $Formula: f_{\text {ind}}:$ $Formula: f_{\text {ind}}:$

Je größer ist, desto kleiner ist die Frequenz $Formula: f_{\text {Feder}},$ $Formula: f_{\text {Feder}},$ mit der die Blattfeder schwingt.
Je kleiner $Formula: f_{\text {Feder}}$ $Formula: f_{\text {Feder}}$ ist, desto kleiner ist die Frequenz $Formula: f_{\text {ind}}$ $Formula: f_{\text {ind}}$ der Induktionsspannung.

Amplitude $Formula: U_{\text {max}}:$ $Formula: U_{\text {max}}:$

Je größer ist, desto kleiner ist die Frequenz $Formula: f_{\text {Feder}},$ $Formula: f_{\text {Feder}},$ mit der die Blattfeder schwingt.
Je kleiner $Formula: f_{\text {Feder}}$ $Formula: f_{\text {Feder}}$ ist, desto kleiner ist die zeitliche Änderung $Formula: \dot{\Phi}$ $Formula: \dot{\Phi}$ des magnetischen Flusses an der Spule.
Je kleiner $Formula: \dot{\Phi}$ $Formula: \dot{\Phi}$ ist, desto geringer ist nach dem Induktionsgesetz der Betrag der Induktionsspannung und damit auch deren Amplitude $Formula: U_{\text{max}}.$ $Formula: U_{\text{max}}.$

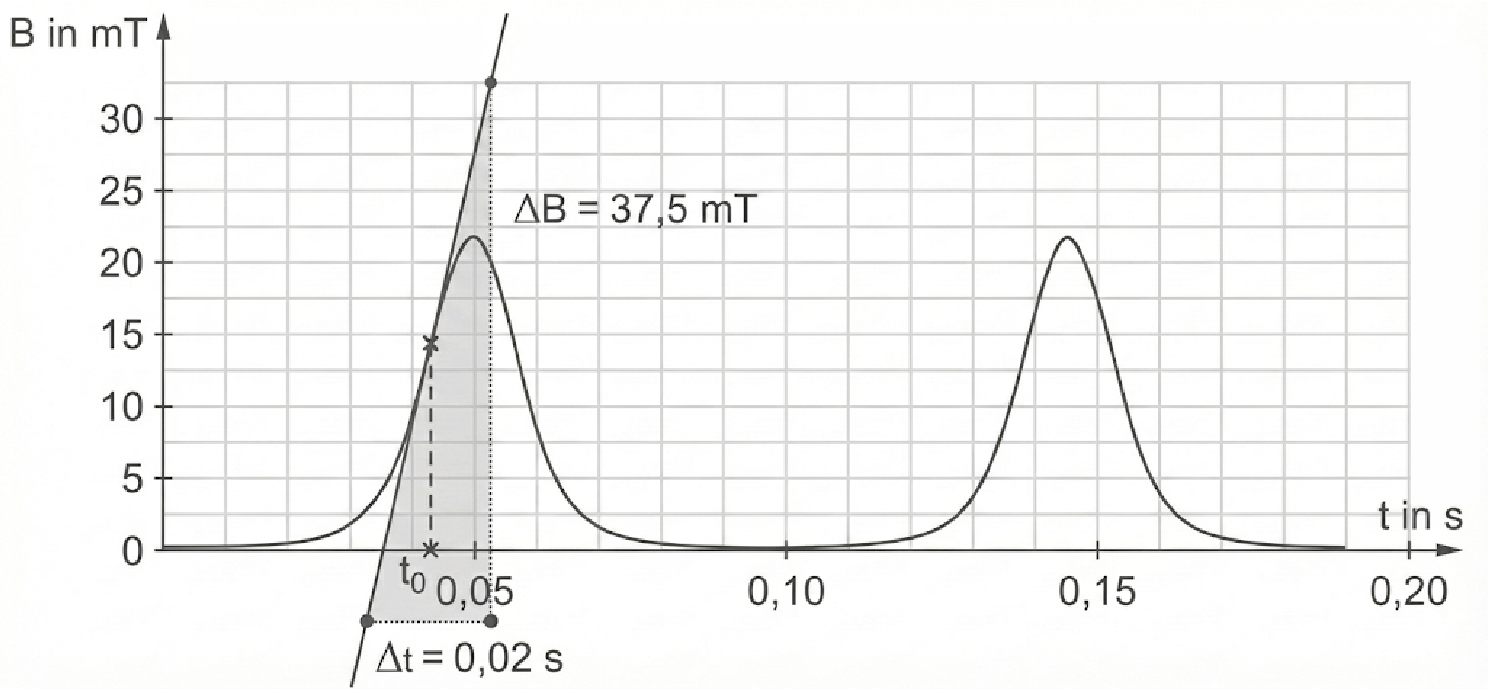
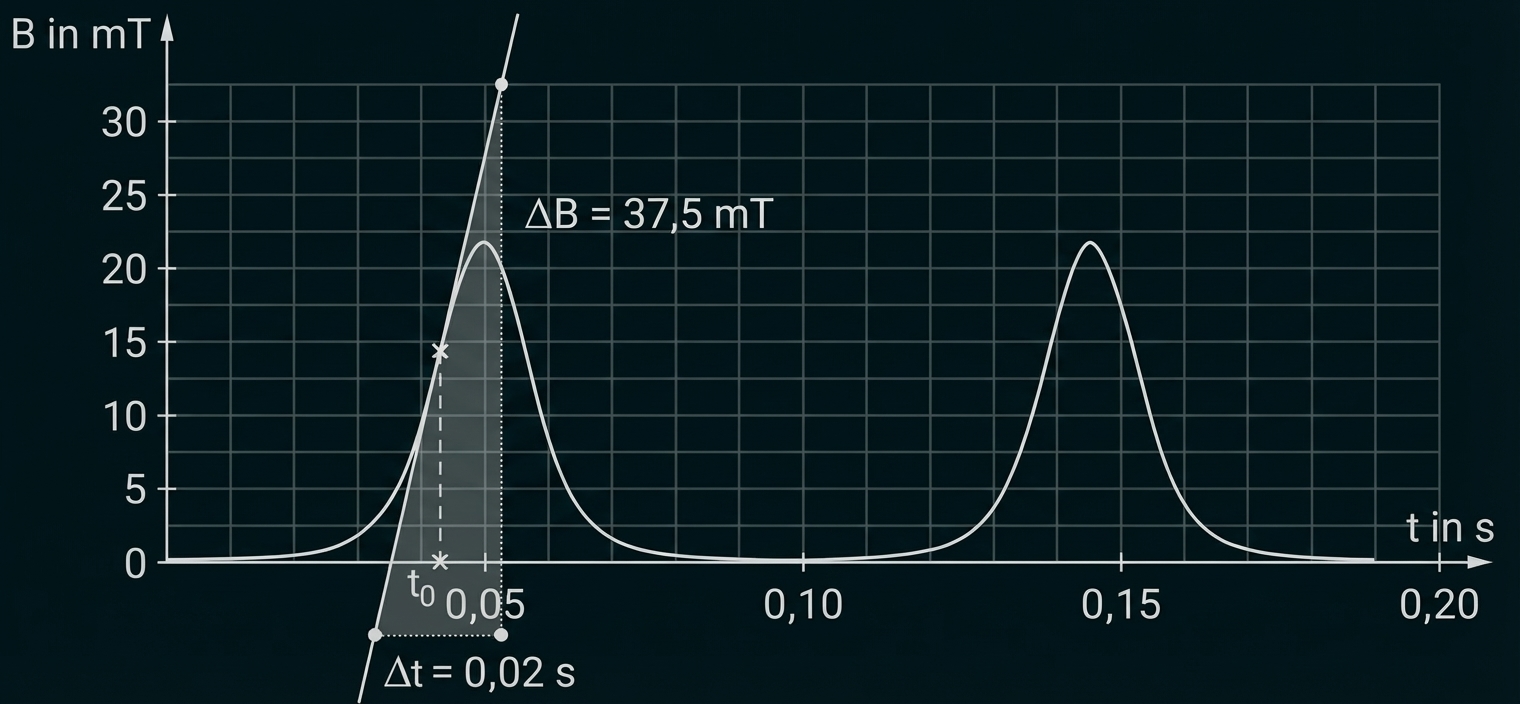
Diagramm: Magnetfeld B in mT über Zeit, zwei Peaks, markierte Fläche beim ersten Peak, Beschriftungen ΔB=37,5 mT und Δt=0,02 s

Dem grau getönten Steigungsdreieck kann entnommen werden, dass während der Zeit $Formula: 0,02\;\mathrm{s}$ $Formula: 0,02\;\mathrm{s}$ die Flussdichte etwa um $Formula: 37,5\;\mathrm{mT}$ $Formula: 37,5\;\mathrm{mT}$ ansteigt, also ist

$Formula: \dot{B}_{\text{max}}=\dfrac{0,0375\;\mathrm{T}}{0,02\;\mathrm{s}}=1,9\;\dfrac{\mathrm{T}}{\mathrm{s}}.$ $Formula: \dot{B}_{\text{max}}=\dfrac{0,0375\;\mathrm{T}}{0,02\;\mathrm{s}}=1,9\;\dfrac{\mathrm{T}}{\mathrm{s}}.$

Nach dem Induktionsgesetz folgt bei zeitlich konstanter Spulenfläche Formula: A:

$Formula: \begin{array}[t]{rll} U_{\text{ind}}\left(t_0\right)&=& -N \cdot \dot{\Phi}\left(t_0\right) \\[5pt] &=& -N \cdot A \cdot \dot{B}_{\max} \\[5pt] &=& -1000 \cdot 16 \cdot 10^{-4}\;\mathrm{m}^2 \cdot 1,9\;\dfrac{\mathrm{T}}{\mathrm{s}} \\[5pt] &=& -3,0\;\mathrm{V} \end{array}$ $Formula: \begin{array}[t]{rll} U_{\text{ind}}\left(t_0\right)&=& -N \cdot \dot{\Phi}\left(t_0\right) \\[5pt] &=& -N \cdot A \cdot \dot{B}_{\max} \\[5pt] &=& -1000 \cdot 16 \cdot 10^{-4}\;\mathrm{m}^2 \cdot 1,9\;\dfrac{\mathrm{T}}{\mathrm{s}} \\[5pt] &=& -3,0\;\mathrm{V} \end{array}$

Damit beträgt die maximal induzierte Spannung $Formula: U_{\max }=3 , 0\;\mathrm{V}.$ $Formula: U_{\max }=3 , 0\;\mathrm{V}.$

Die Messkurve in Material 4 Abb. 5, die der Modellrechnung zugrunde liegt, zeigt den Formula: B(t) -Verlauf im Punkt Formula: Q, der am dem Magneten zugewandten Ende der Spulenachse liegt. Die Spule besitzt eine Länge, die in der Größenordnung des Abstands Formula: d zwischen Magnet und Spule liegt und nicht vernachlässigt werden kann; daher nimmt längs der Spulenachse der Betrag der magnetischen Flussdichte deutlich ab. Damit fällt auch die zeitliche Änderung der Flussdichte innerhalb der Spule und damit der Maximalbetrag $Formula: U_{\max}$ $Formula: U_{\max}$ der induzierten Spannung deutlich kleiner als in der Modellrechnung aus.

Würden Magneten so an den Gitarrensaiten befestigt werden, würden diese beim Spiel sich ggf. gegenseitig stoßen oder gar aneinanderhaften, weil sie sich gegenseitig anziehen. Die Spielbarkeit ist eingeschränkt. Zudem würden sich durch die befestigten Magneten auch das Schwingungsverhalten und damit die Klangeigenschaften ändern. Diese Bauweise ist also aus Sicht eines Gitarrenspielers ungeeignet.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?