A3 Quantenobjekte
Interferenzexperimente sind eine wesentliche Methode zur Untersuchung von Quantenobjekten. Am Beginn standen Experimente mit Elektronen. In den vergangenen Jahrzehnten wurden solche Experimente auch mit zunehmend größeren Objekten durchgeführt.
An der Universität Wien wurde 2012 die Interferenz von Farbstoffmolekülen an einem Gitter untersucht. Zunächst werden nur Farbstoffmoleküle mit einheitlicher Geschwindigkeit betrachtet.
Skizziere einen Versuchsaufbau, bei dem durch ein elektrisches und ein magnetisches Feld erreicht wird, dass einfach positiv geladene Farbstoffmoleküle diesen Versuchsaufbau nur mit dem Geschwindigkeitsbetrag von passieren können. Trage in die Skizze dafür notwendige Messgrößen ein und gib passende Werte an.
Zeige mithilfe der Tabelle in Material 1, dass ein Farbstoffmolekül mit dem Geschwindigkeitsbetrag von eine De-Broglie-Wellenlänge von
besitzt.
In Material 1 ist der 2012 durchgeführte Interferenzversuch beschrieben. Skizziere die Intensitätsverteilung entlang der Linie die sich aus dem Schirmbild in Material 1 Abb. 2 ergibt.
Das in Material 2 Abb. 3 dargestellte Verfahren erlaubt die Bestimmung der Intensität an einem beliebigen Punkt auf der Linie Erläutere dieses Verfahren. Gib für das Beispiel in Material 2 die Anzahl der Spalte an, die vom Molekülstrahl getroffen wurden. Ermittele für Moleküle mit der De-Broglie-Wellenlänge aus Teilaufgabe b die Differenz der Weglängen von den Spaltmitten zweier benachbarter Spalte zum Schirmpunkt.
Bestimme anhand von Material 1 Abb. 2 den Abstand des Schirms vom Gitter und schätze die Messunsicherheit des Ergebnisses ab. Erläutere eine notwendige Näherung bei der Bestimmung von
mit den daraus abgeleiteten Vereinfachungen.
Trotz des in Teilaufgabe a entwickelten Aufbaus besitzen die Farbstoffmoleküle im realen Experiment leicht unterschiedliche Geschwindigkeiten um den Mittelwert herum.
Begründe, dass die Auftreffpunkte auf den Linien und
(siehe Material 1 Abb. 2) zu Molekülen mit unterschiedlichen Anfangsgeschwindigkeiten
und
gehören. Erkläre damit, dass die zu den Maxima 1. Ordnung gehörenden Interferenzstreifen nicht parallel sind.
Viele Quanteneigenschaften des Photons lassen sich mit Interferometer-Experimenten untersuchen.
Erläutere die Koinzidenzmethode zur Präparation einzelner Photonen und Durchführung von Experimenten mit einzelnen Photonen.
In ein Mach-Zehnder-Interferometer werden, wie in Material 3 dargestellt, nichtlineare Kristalle eingebaut. Erläutere die daraus resultierende Änderung des Messergebnisses.
Beurteile den Werbeflyer in Material 4 hinsichtlich seiner Vertrauenswürdigkeit. Berücksichtige die verwendete Argumentationsstruktur.
Material 1: Interferenz von Farbstoffmolekülen
Die Farbstoffmoleküle bewegen sich vor dem Gitter genau auf den Ursprung des -
-Koordinatensystems des Schirms zu und treffen senkrecht auf das Gitter. Der Schirm ist parallel zum Gitter im Abstand
angeordnet (siehe Abb. 1).
Abb. 2 zeigt maßstabsgetreu das sich ergebende Interferenzbild auf dem Schirm. Die Geschwindigkeit der Moleküle ist so gering, dass der Einfluss der Gewichtskraft in negativer -Richtung berücksichtigt werden muss.
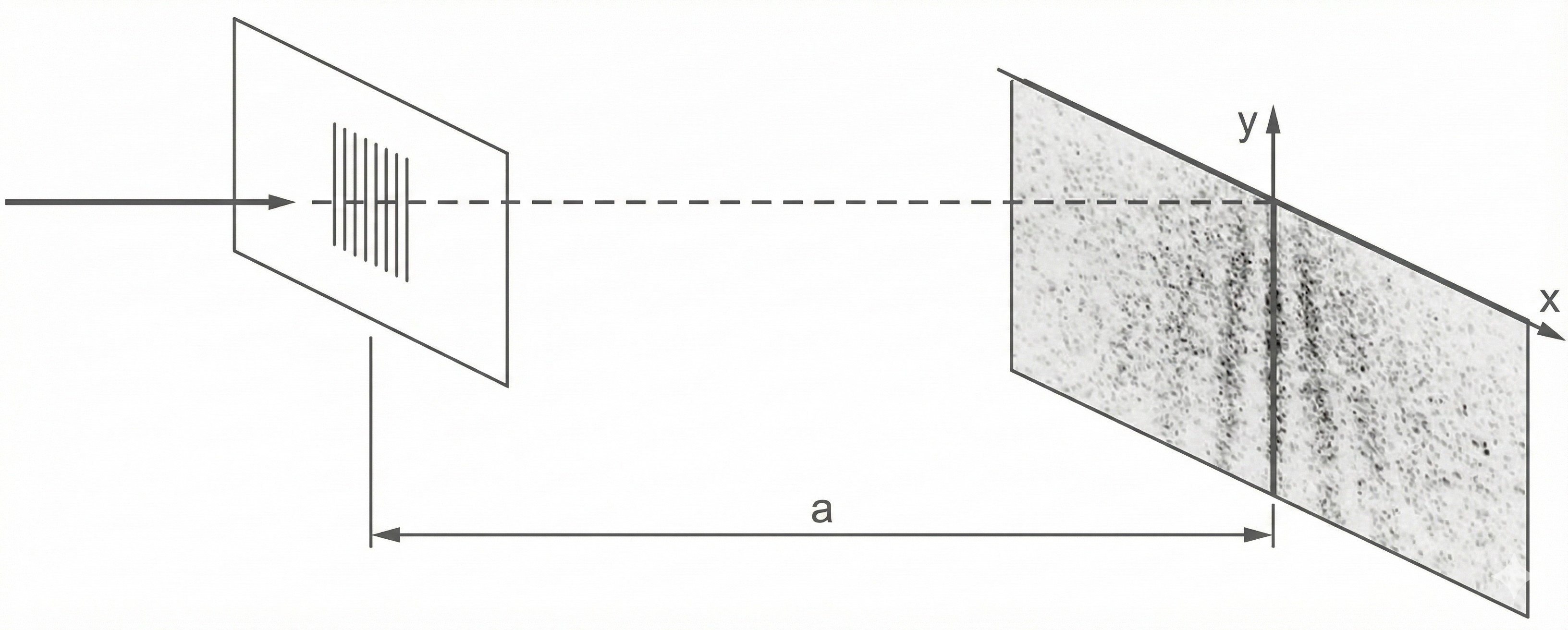
Abb. 1: Versuchsaufbau
|
Masse eines Farbstoffmoleküls |
|
|
Summenformel eines Farbstoffmoleküls |
|
|
Geschwindigkeit der Farbstoffmoleküle |
|
|
Spaltmittenabstand |
|
|
Schirmbreite |
|
Daten des Experiments
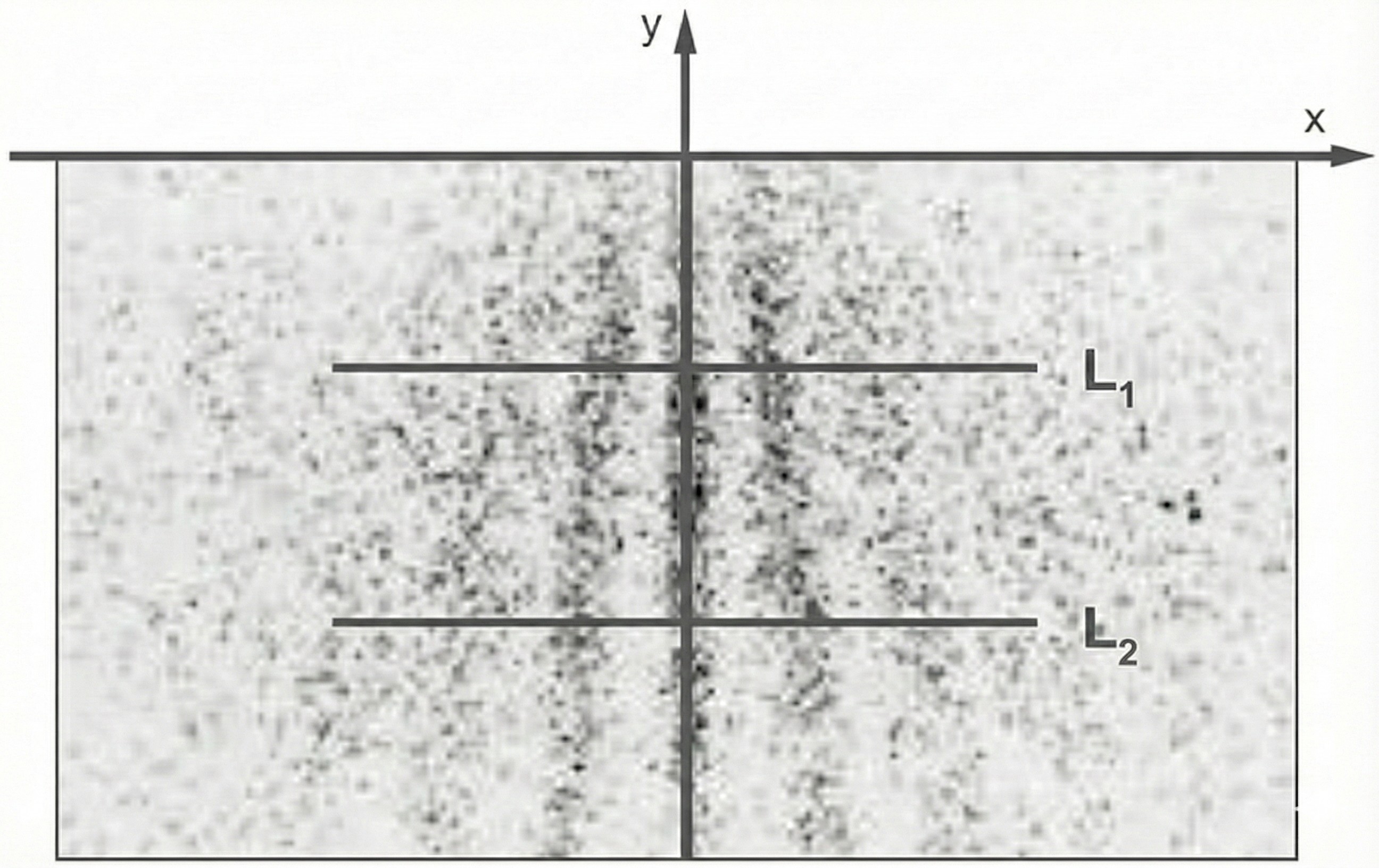
Abb. 2: maßstabsgetreues Schirmbild
(Abb. 1 und Abb. 2 sind in Anlehnung an Thomas Juffmann, Adriana Milic, Michael Müllneritsch, Peter Asenbaum, Alexander Tsukernik, Jens Tüxen, Marcel Mayor, Ori Cheshnovsky and Markus Arndt:
Real-time single-molecule imaging of quantum interference.
In: Nature Naonotechnology Vol 7, Mai 2012)
Material 2: Verfahren zur Intensitätsbestimmung
Abb. 3 zeigt das Zwischenergebnis eines Verfahrens, mit dessen Hilfe die Intensität des Interferenzbilds an einem bestimmten Punkt auf dem Schirm ermittelt werden kann.
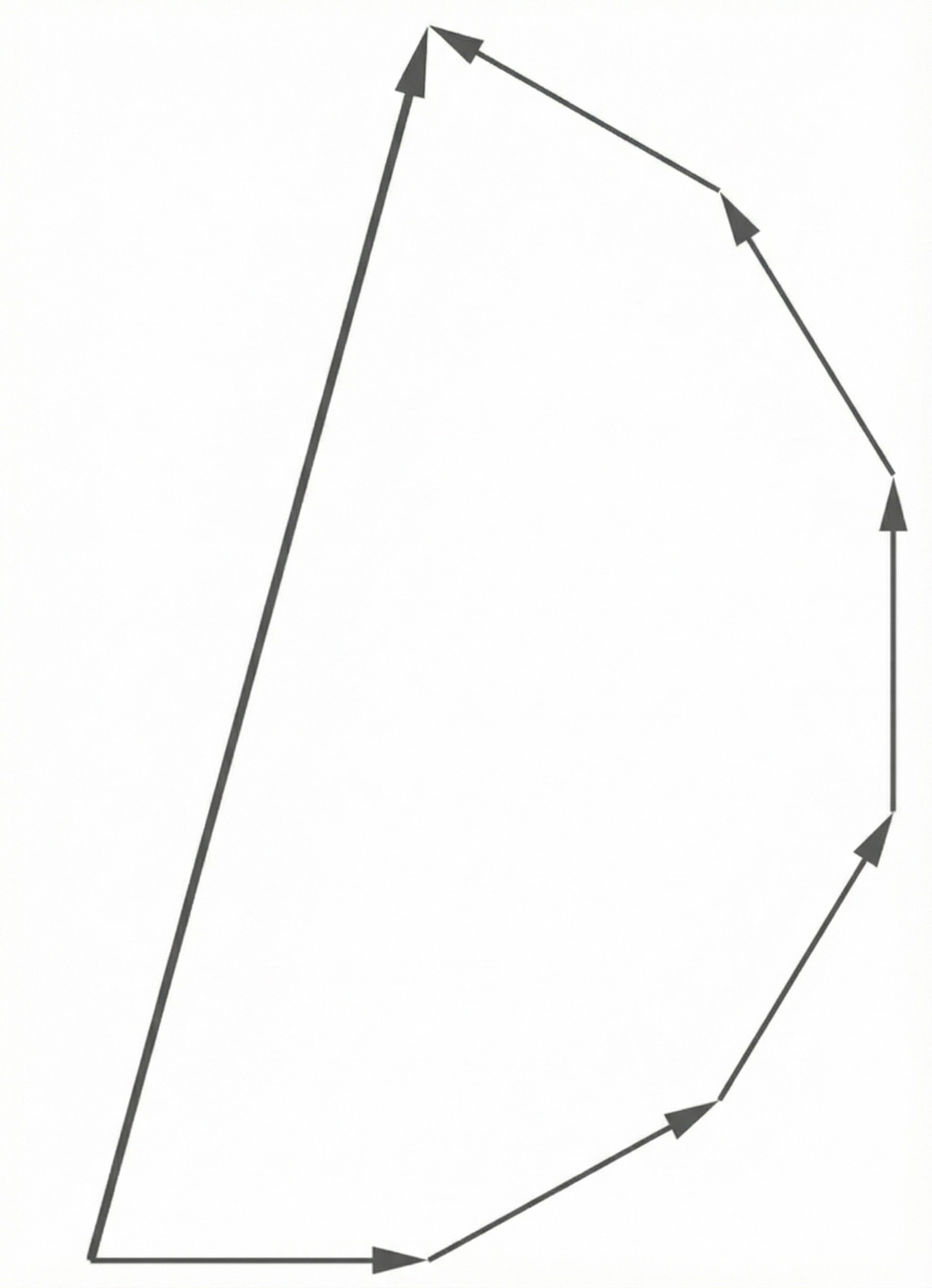
Abb. 3
Material 3: Photonenverdopplung im Mach-Zehnder-Interferometer
Um ein einzelnes Photon im Mach-Zehnder-Interferometer zu verfolgen, bietet sich die Methode der Photonenverdopplung an. Dazu wird ein nichtlinearer Kristall in den Lichtweg gesetzt, der das ankommende Photon absorbiert und zwei identische Photonen geringerer Energie in unterschiedliche Richtungen emittiert (siehe Abb. 4).
Bringt man in beide Wege des Interferometers solche Kristalle ein (siehe Abb. 5), so ändert sich die Wegdifferenz nicht. Trifft nun ein Photon auf einen der beiden Kristalle, so durchläuft eines der im Kristall erzeugten Photonen weiterhin das Interferometer, während das andere detektiert werden kann und damit anzeigt, von welchem der beiden Kristalle das ursprüngliche Photon absorbiert wurde.
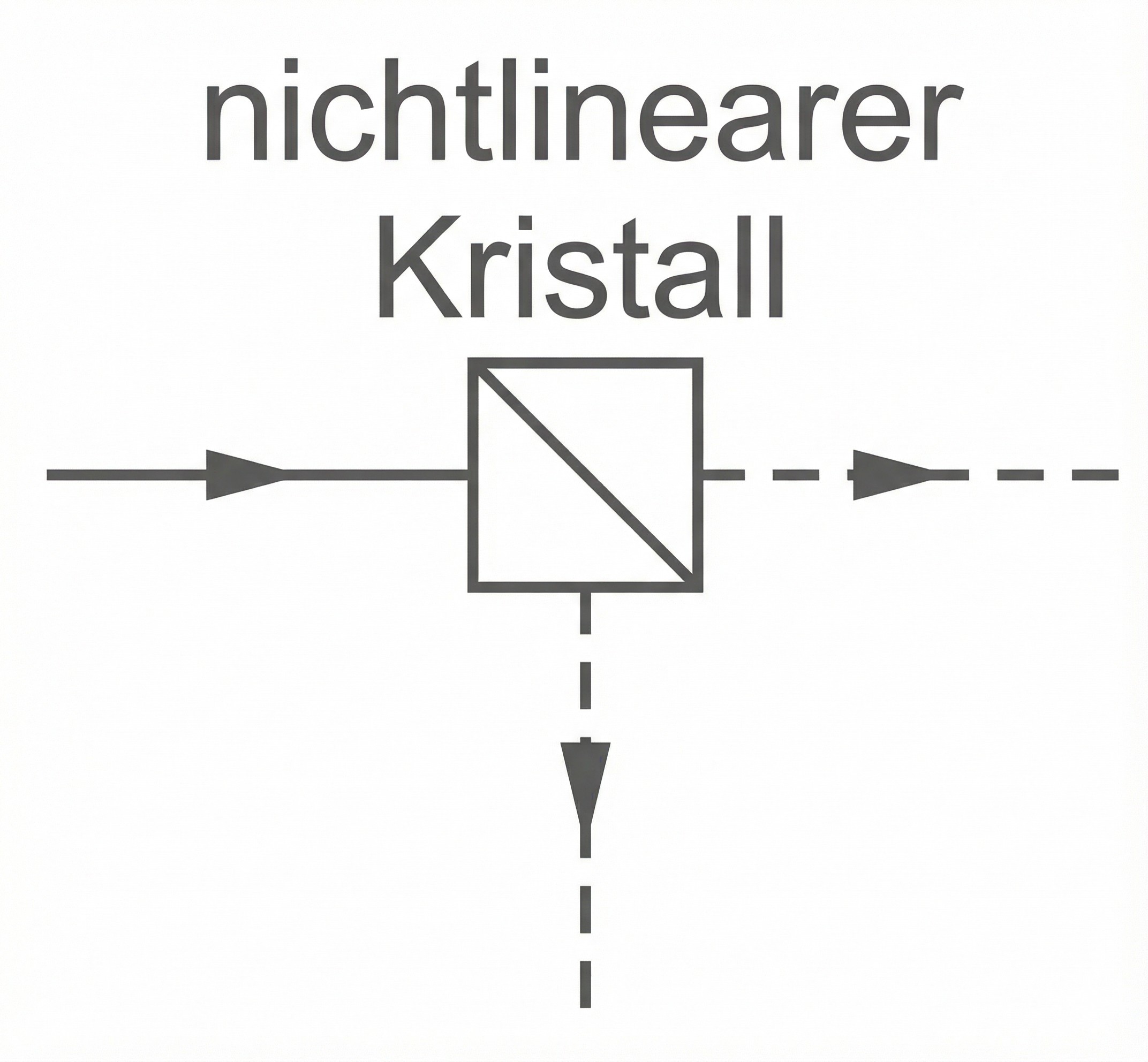
Abb. 4: Das einfallende Photon (durchgezogene Linie) erzeugt im nichtlinearen Kristall zwei identische Photonen (gestrichelte Linien).
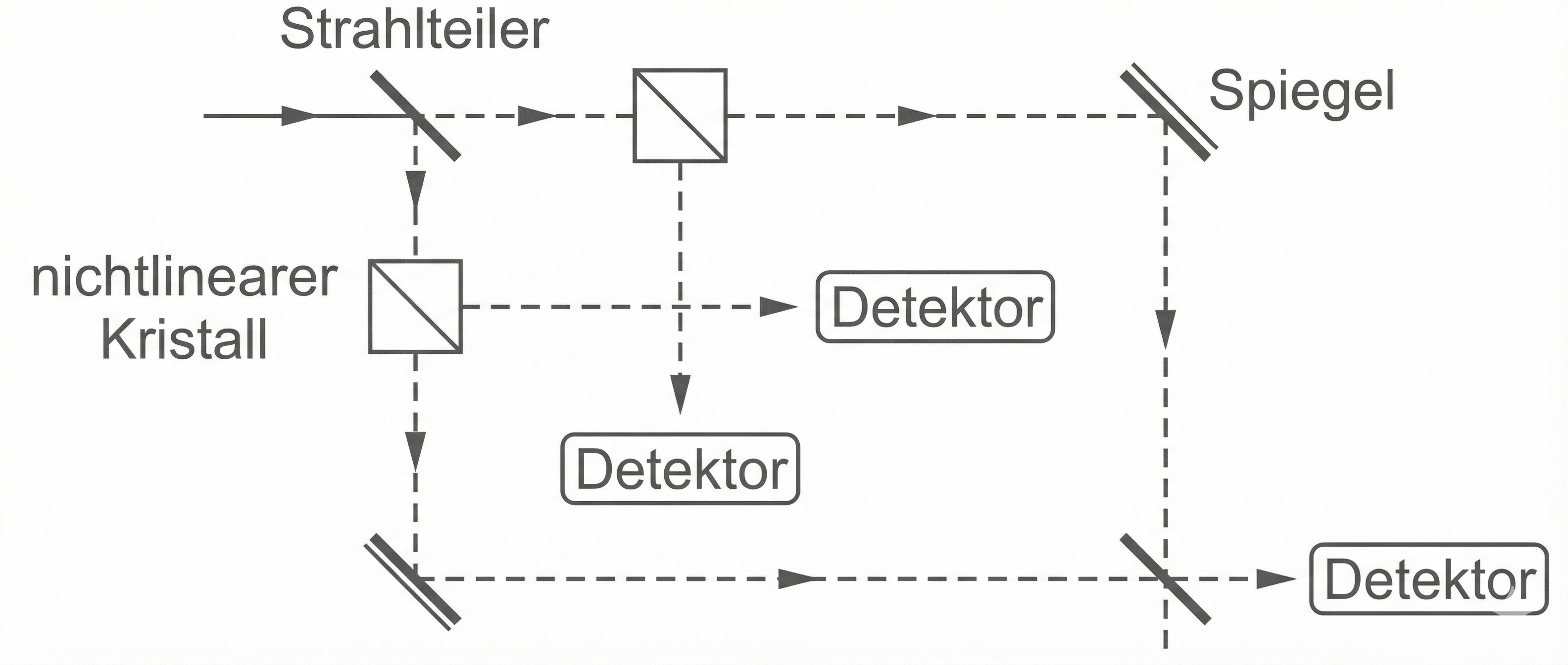
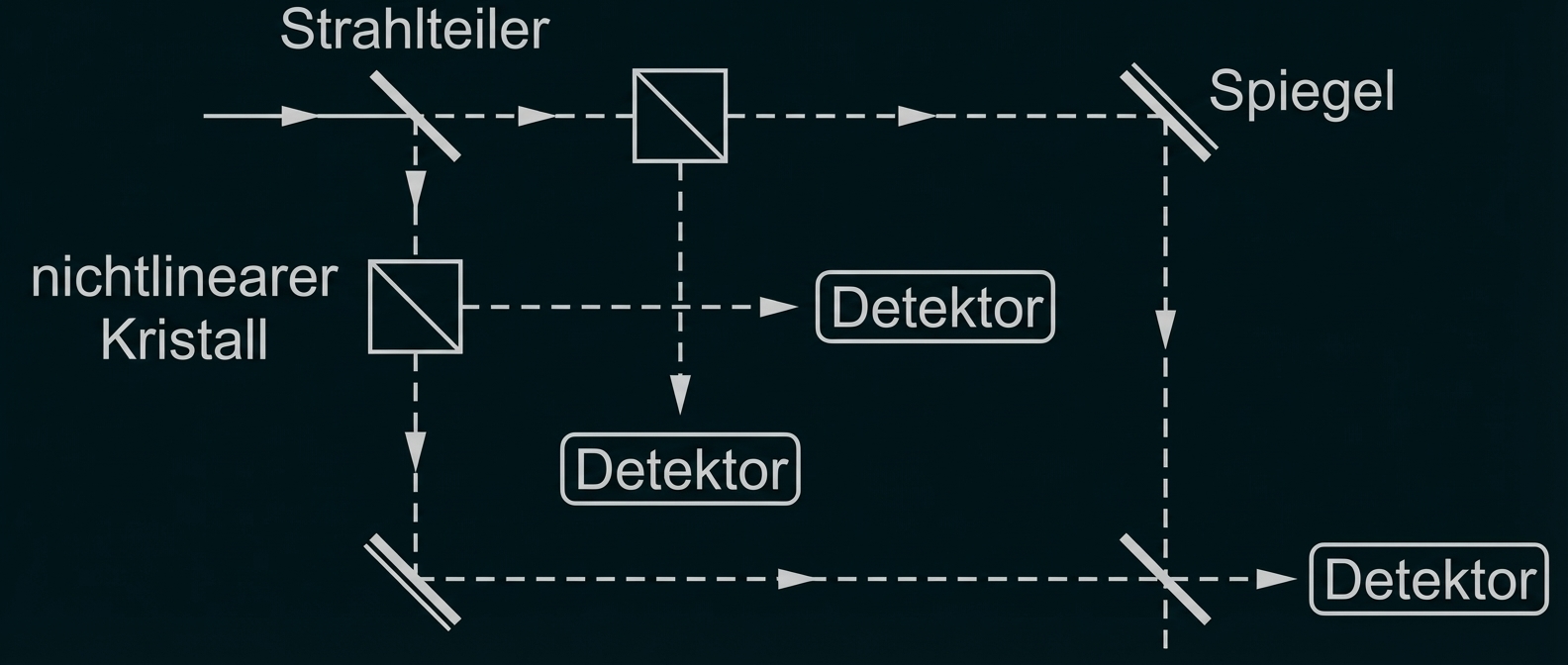
Abb. 5: Detektion des Lichtwegs im Interferometer
Material 4: Werbeflyer
NoAtoS – Der neue Atomstrom-StopperTrotz der Abschaltung aller deutschen Atomkraftwerke haben wir wegen Stromimporten aus dem Ausland weiterhin Atomstrom im deutschen Netz. Wollen Kundinnen und Kunden sichergehen, keinen Atomstrom in ihren Geräten zu haben? Dann bietet sich folgende Lösung an: NoAtoS – der neuartige Atomstrom-Stopper!!! Der Erfindergeist von Dr. Scharlan nutzt die Gesetze der Quantenphysik genial aus: NoAtoS detektiert zuverlässig eine im stochastischen Verhalten der Elektronen hinterlegte Information, die sich auch mit von der Atomlobby eingesetzten Quantenradierern nicht löschen lässt. Die geniale Idee dahinter: Die bei der Kernspaltung freigesetzte große Energie wird durch Interferenzeffekte auf weitere Elektronen des Stroms übertragen und kündigt damit ankommenden Atomstrom bei NoAtoS an. Die ausgefeilte Technik des NoAtoS erkennt dies nach dem Komplementaritätsprinzip, stoppt den Atomstrom zuverlässig und leitet ihn wieder an den Produzenten zurück. 

Die Atomindustrie kann an den Kundinnen und Kunden nichts mehr verdienen! Der NoAtoS-Atomstrom-Stopper wird in einem formschönen Gehäuse ausgeliefert und kann bei jedem Endgerät zwischen Steckdose und Gerät eingebaut werden. Bestelle den persönlichen NoAtoS jetzt! 

|
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Ein Wienfilter liefert als Geschwindigkeitsfilter die gewünschten Ergebnisse. Die Skizze unten zeigt einen möglichen Aufbau. Die einfach positiv geladenen Farbstoffmoleküle erfahren im elektrischen Feld des Plattenkondensators die elektrische Ablenkungskraft nach unten sowie die betragsgleiche Lorentzkraft
nach oben.
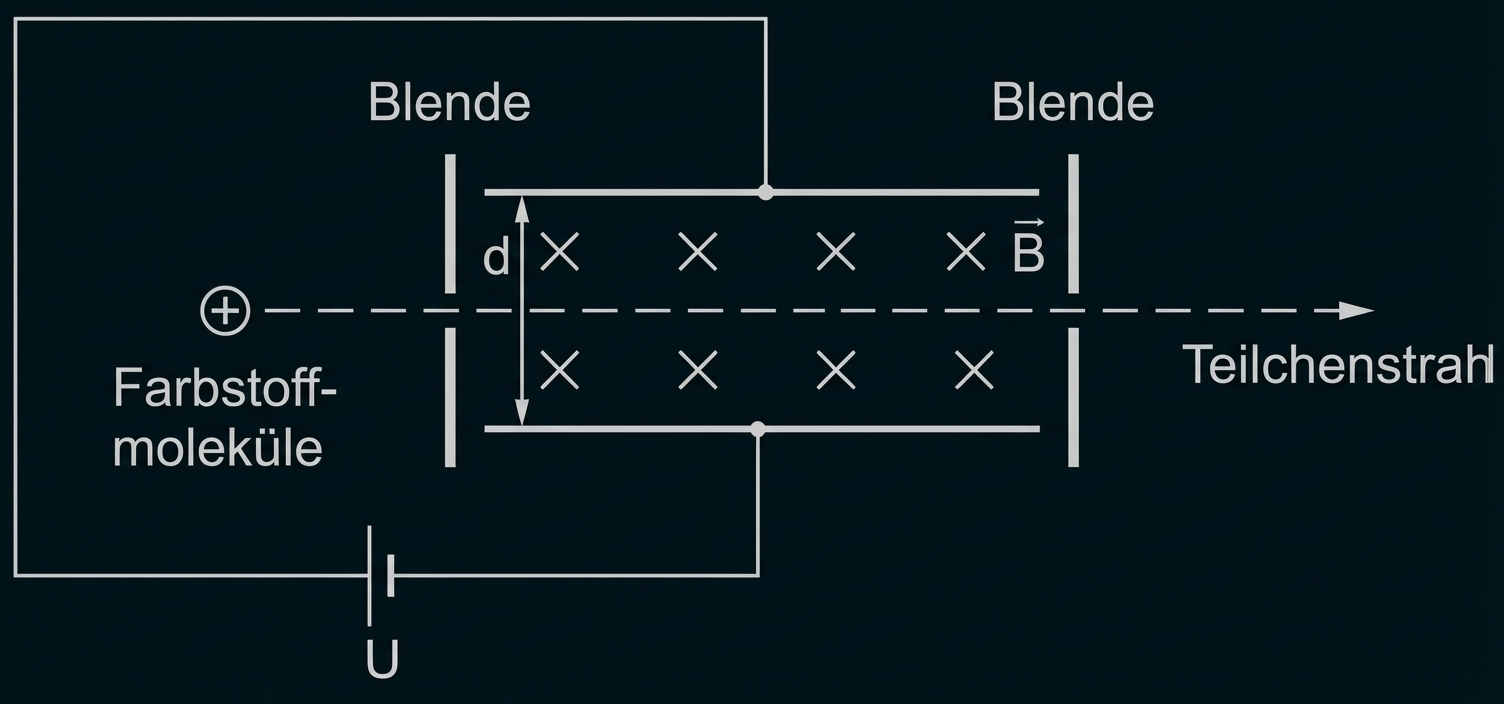
Im Kräftegleichgewicht gilt
d. h., es gelangen nur die Teilchen durch die Lochblende, deren Geschwindigkeit den durch die obige Formel festgelegten Betrag besitzt. Werden z. B. für den Plattenabstand und für die Flussdichte
gewählt, dann wird der vorgegebene Geschwindigkeitsbetrag von
für die Kondensatorspannung
erzielt.
Für die De-Broglie-Wellenlänge der Moleküle gilt die Beziehung:
Mit der Molekülmasse aus der Tabelle von Material 1 folgt:
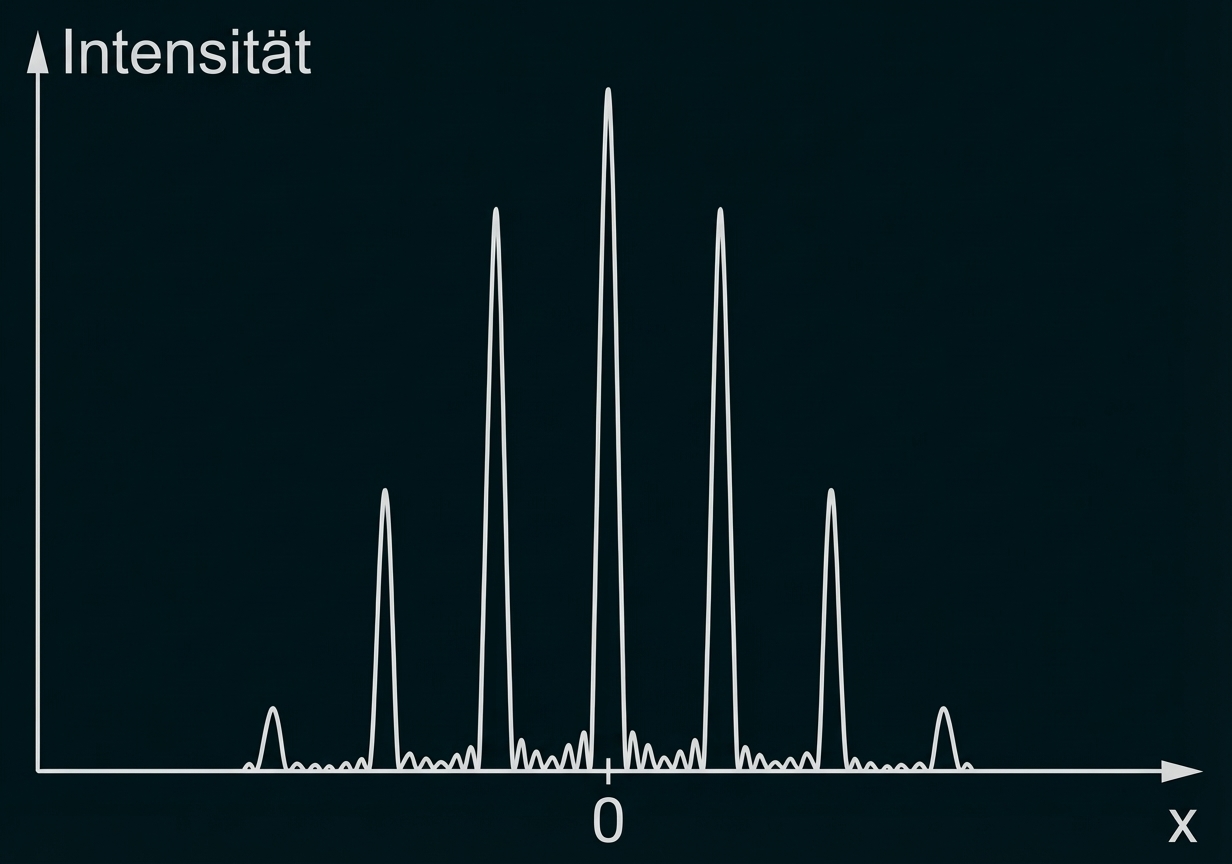
Abb. 3 in Material 2 zeigt ein Zeigerdiagramm mit 6 gleich langen, aber jeweils um einen Winkel von gedrehten Pfeilen (=Zeiger). Jeder der Zeiger veranschaulicht eine Welle, die von einem Spalt ausgeht und am gleichen Punkt am Schirm eintrifft. Dabei gilt:
-
Die Pfeillänge gibt die Wellenamplitude an. Sie ist hier für alle 6 Wellenzüge gleich groß.
-
Der Winkel zwischen den Pfeilen gibt die Phasenbeziehung der eintreffenden Wellen an. Im vorliegenden Fall besteht ein fester Phasenunterschied von
zwischen benachbarten Zeigern.
-
Der Phasenunterschied beschreibt den Gangunterschied der Wellen, wobei der Vollwinkel
einer ganzen Wellenlänge
entspricht.
Die im Punkt resultierende Amplitude der sich dort überlagernden Wellen lässt sich durch vektorielle Addition ermitteln; sie ist in Abb. 3 dargestellt. Die resultierende Amplitude entspricht der Länge des (fett gezeichneten) Summenpfeils. Die Intensität im Punkt
ist dann gleich dem Quadrat dieser Amplitude. Im Beispiel liegen 6 Spalte vor, die vom Molekülstrahl getroffen werden. Als Gangunterschied
zwischen den Wellen aus Nachbarspalten ergibt sich wegen
der zwölfte Teil der in Teilaufgabe b berechneten De-Broglie-Wellenlänge:
Aus der Abb. 2 erhält man als Messwerte eine Schirmbreite von die Maxima zweiter Ordnung haben einen Abstand von
(Schirmoberkante) bis
(Schirmunterkante). Wegen der Maßstabstreue lassen sich mithilfe der realen Schirmbreite von
die realen Abstände berechnen:
und
Der Abstand von 0. zum 2. Maximum liegt dann im Bereich zwischen
und
Für den Gangunterschied beim 2. Maximum folgt:
Für den Schirmabstand folgt mittels der Beziehung
je nach verwendetem Wert für dann
-
minimal:
-
maximal:
Für den gemessenen Schirmabstand ergibt sich somit:
Bei der Bestimmung von werden folgenden Näherungen angewendet:
-
stellt die Beugungsbedingung für konstruktive Interferenz dar. Ihre Gültigkeit leitet sich aus der Winkelbeziehung im rechtwinkligen Dreieck ab, das gebildet wird, wenn die Verbindungslinien zwischen den Spaltmitten und dem Auftreffpunkt am Schirm als parallel angenommen werden. Diese Annahme ist nur gerechtfertigt, wenn wie hier der Schirm-
abstand
sehr viel größer als der Spaltmittenabstand
ist:
-
gibt die geometrische Lagebeziehung von Schirmabstand
und dem Maximumabstand
wieder. Die trigonometrische Beziehung ist nur erfüllt, wenn
angenommen werden darf, was hier wegen
der Fall ist.
Besitzen zwei Moleküle 1 und 2 unterschiedliche Anfangsgeschwindigkeiten , so erfährt das langsamere Molekül 1 während des Flugs zum Schirm länger die Gravitationskraft; folglich erreicht es den Schirm weiter unten als Molekül 2 (unterschiedliche vertikale Ablenkung).
Die De-Broglie-Wellenlänge ist umgekehrt proportional zur Teilchengeschwindigkeit. Daher haben langsamere Moleküle eine größere Wellenlänge und damit wegen der Beugungsbedingung
einen größeren Abstand zwischen den Maxima. Folglich erreicht Molekül 1 den Schirm weiter außen als Molekül 2 (unterschiedliche horizontale Ablenkung).
Beide Ablenkungen führen dazu, dass die Interferenzstreifen erster Ordnung nicht parallel sind, wie es in Abb. 2 zu sehen ist.
Die Idee der Koinzidenzmethode besteht darin, dass man für die Vermessung einzelner Photonen zwei Photonen betrachtet, nämlich das eigentlich zu vermessende Photon und zusätzlich ein zweites "Kontrollphoton". Beide werden zeitgleich erzeugt, aber nach Durchlauf der Messanordnung an verschiedenen Orten detektiert. Geschieht die Detektion praktisch zeitgleich (innerhalb von wenigen Nanosekunden), ist die Koinzidenz (wörtlich: „Zusammenfallen“) der beiden Messereignisse erfüllt. Sie stellt sicher, dass tatsächlich das betrachtete Einzelphoton vermessen wurde und nicht etwa ein anderes Störereignis die Detektion ausgelöst hat.
Voraussetzung ist die Erzeugung zweier identischer Photonen. Das gelingt zum Beispiel mithilfe eines nichtlinearen Kristalls (vgl. Material 3): Dieser sendet nach Anregung durch einen Laser zwei identische Photonen mit halber Energie des anregenden Laserphotons aus.
Laut dem Text in Material 3 lässt sich mit der gezeigten Versuchsanordnung durch Messung des Kontrollphotons zeigen, von welchem der beiden Kristalle das ursprüngliche Photon absorbiert wurde, und damit der Weg feststellen, den das am Detektor (rechts unten in Abb. 5) registrierte Photon genommen hat. Durch diese zuverlässige (Koinzidenz!) Lokalisierung geht die Superposition möglicher Zustände verloren und es ergibt sich kein Interferenzmuster.
Der Verfasser beschreibt zunächst die angebliche Wirkung seines Produktes, die darin bestehen soll, Atomstrom von angeschlossenen elektrischen Geräten fernzuhalten. Die im restlichen Text des Flyers genannten Argumente sind aus mehreren Gründen nicht stichhaltig:
-
Der Verfasser reiht verschiedene physikalische Fachbegriffe wie „stochastisches Verhalten der fließenden Elektronen“, „Quantenradierer“, „Interferenzeffekte" oder "Komplementaritätsprinzip" zusammenhanglos aneinander.
-
Die angeführten Argumente klingen physikalisch, sind aber fachlich falsch: So kann etwa Energie nicht, wie behauptet, aufgrund von Interferenzeffekten auf die Elektronen des Stroms übertragen werden; ebenso wenig lässt das Vorhandensein von Energie auf die Energiequelle schließen oder erlaubt das stochastische Verhalten von Elektronen die Übertragung von Informationen.
-
Der angebliche Doktortitel des Erfinders und die vermeintliche Fachsprache suggerieren eine Seriosität, die der Stil des Textes nicht halten kann: weder durch die unsachliche Wortwahl („Atomlobby“), die plakative Zeichensetzung („Atomstrom-Stopper!!!“), das eher politisch motivierte Logo oben rechts noch durch den populistischen Ton („Die Atomindustrie kann an Ihnen nichts mehr verdienen!").
Insgesamt erweist sich der Flyertext als marktschreierische Ansammlung bloßer Behauptungen, die physikalisch nicht fundiert sind, und wirkt damit absolut nicht vertrauenswürdig.