A5 Induktionsschleifen im Straßenverkehr
In Fahrbahnen ist gelegentlich an Schnitten im Straßenbelag zu erkennen, dass im Untergrund eine mehr oder weniger rechteckige Leiterschleife verlegt ist (vgl. Material 3 Abb. 3). Solche „Induktionsschleifen“ werden verwendet, um beispielsweise Grünlicht an Ampeln auszulösen. Die physikalische Grundlage der im Folgenden betrachteten technischen Umsetzung ist der elektromagnetische Schwingkreis.
In Material 1 ist dargestellt, dass der elektromagnetische Schwingkreis analog zum horizontalen Federpendel betrachtet werden kann.
Veranschauliche in Material 1 Abb. 1 für alle vier Zeitpunkte die elektrischen und magnetischen Felder im Bereich von Kondensator und Spule durch Feldlinien.
Begründe, dass in dieser Analogie die Auslenkung des Federpendels aus der Ruhelage der Ladung des Kondensators entspricht.
Ermittle die Frequenz der in Material 2 dargestellten Schwingung möglichst genau und berechne den Wert der Stromstärke zum Zeitpunkt
Bestätige mithilfe der Thomson’schen Schwingungsgleichung, dass die Induktivität der verwendeten Induktionsschleife etwa beträgt.
Wenn sich ein Gegenstand oberhalb der zum elektromagnetischen Schwingkreis gehörenden Induktionsschleife befindet, kann das zu einer Beeinflussung des dortigen Magnetfelds sowie einer Änderung der Induktivität im Vergleich zum Schwingkreis ohne Gegenstand führen. Der Schwingkreis wird „verstimmt“ (siehe Material 3).
In Fahrzeugen ist in der Regel Eisen verbaut, welches sowohl ferromagnetisch als auch elektrisch leitfähig ist. Beschreibe für diese beiden Materialeigenschaften jeweils die Auswirkung auf die magnetische Flussdichte oberhalb der Induktionsschleife, wenn sich dort nun ein eisenhaltiges Fahrzeug befindet.
Stelle eine Hypothese auf, die die unterschiedliche Verstimmung durch Pkw bzw. Lkw (siehe Material 3 Tab. 1) erklärt.
Beschreibe einen Versuch, mit dem du diese Hypothese testen kannst – die momentane Schwingkreisfrequenz kannst du dabei direkt an einem Messgerät ablesen.
In der Praxis gelingt die Erkennung von Fahrrädern mit Induktionsschleifen nicht immer.
Zeige rechnerisch, dass eine relative Veränderung der Schwingungsfrequenz von die nach Herstellerangaben für ein Signal ausreicht, durch ein Fahrrad nicht in jedem Fall erreicht wird. Verwende Material 3 und die Thomson’sche Schwingungsgleichung.
Eine fahrradfahrende Mitschülerin fragt: „Wohin soll ich mich an der Ampel mit Induktionsschleife stellen, damit sie mich auf dem Fahrrad möglichst zuverlässig erkennt und Grün gibt?“
Erkläre ihr, warum die rechte Position in Material 4 Abb. 4 hierfür günstiger ist als die linke. Skizziere zur Unterstützung deiner Argumentation in Material 4 Abb. 4 einige magnetische Feldlinien des Feldes der Induktionsschleife.
Ein Hersteller von Induktionsschleifen kritisiert die Idee, zugunsten der Erkennung von Fahrrädern die Empfindlichkeit der Auswerteelektronik maximal zu erhöhen (siehe Material 5).
Diskutiere, ob bei einer Verkehrsampel durch Maximierung der Empfindlichkeit das Risiko von häufigeren Störungen akzeptiert werden sollte, und gib eine Handlungsempfehlung für den Betreiber der Ampelanlage.
Material 1: Mechanische Analogie zum elektromagnetischen Schwingkreis
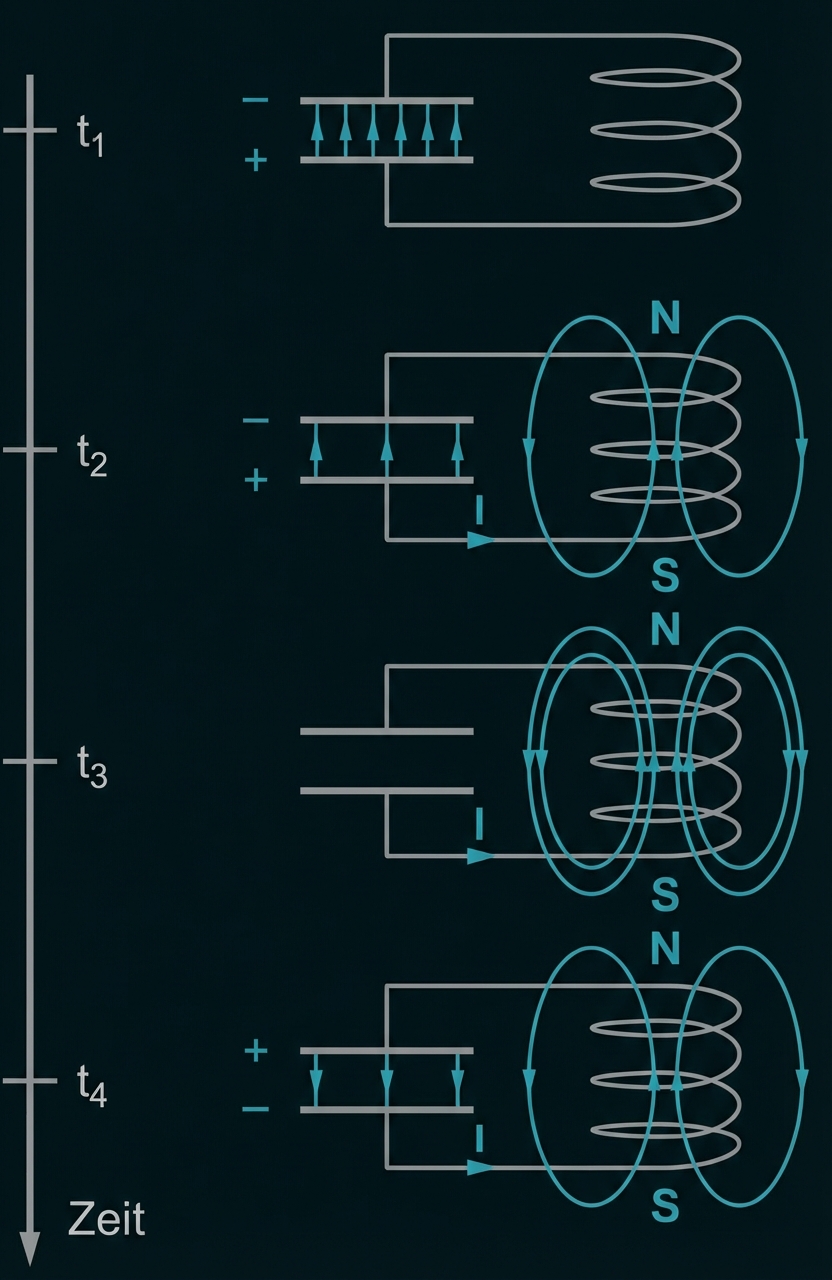
Die ungedämpfte harmonische Schwingung eines horizontalen Federpendels mit zwei gleichartigen Federn, das sich auf einer horizontalen Unterlage bewegt und bei dem daher die Gravitation keine Rolle spielt, ist eine mechanische Analogie zur ungedämpften Schwingung eines elektromagnetischen Schwingkreises. Die Momentangeschwindigkeit des Pendelkörpers ist die analoge Größe zur momentanen Stromstärke im Schwingkreis.
In Abb. 1 sind vier aufeinanderfolgende Phasen einer ungedämpften harmonischen Schwingung eines Federpendels im zeitlichen Verlauf dargestellt. Das System aus Federn und Pendelkörper ist rechts und links befestigt. Zum Zeitpunkt ist die Auslenkung des Pendelkörpers maximal und die obere Platte des Kondensators maximal negativ geladen.
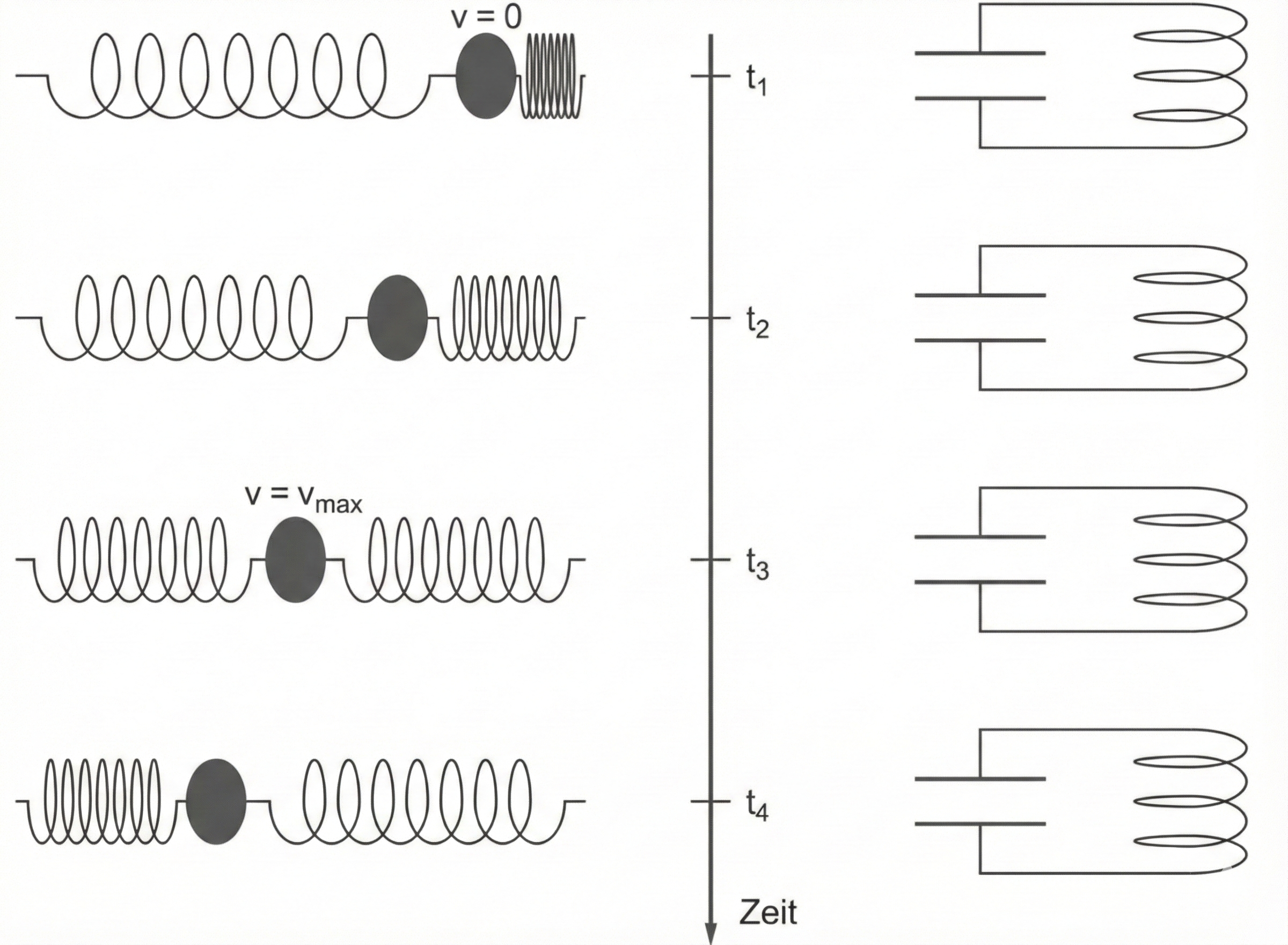
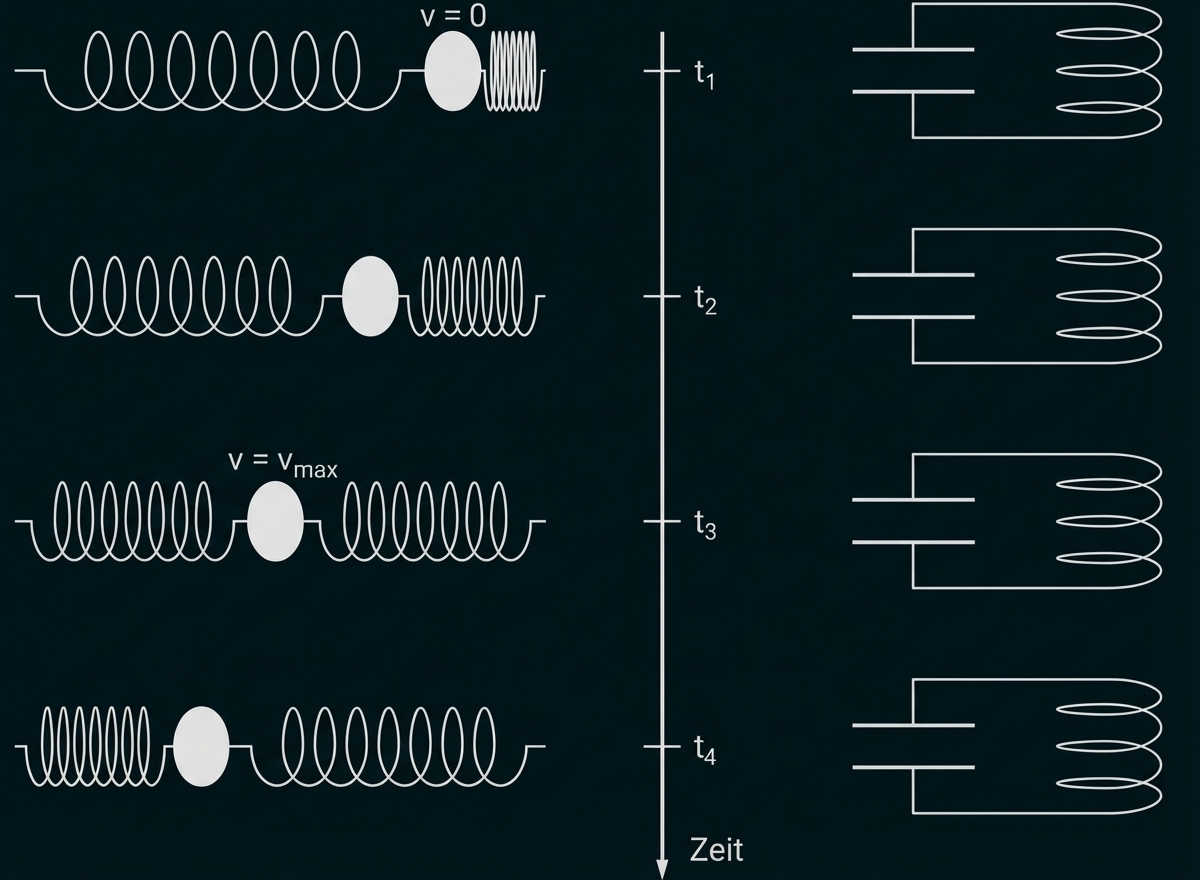
Abb. 1: Analogiebetrachtung von Federpendel und Schwingkreis für vier ausgewählte Zeitpunkte
Material 2: Schwingkreis im Untergrund
Eine Induktionsschleife aus mehreren Drahtwindungen ist unter der Fahrbahnoberfläche verlegt. Sie bildet zusammen mit einem Kondensator der Kapazität einen elektromagnetischen Schwingkreis.
Abb. 2 zeigt die Zeitabhängigkeit der Stromstärke einer idealisierten, ungedämpften elektromagnetischen Schwingung in diesem Schwingkreis.


Abb. 2
Material 3: Verstimmung der Induktionsschleifen
Ein in der Induktionsschleife fließender Wechselstrom erzeugt ein sich periodisch änderndes Magnetfeld. Wenn sich ein Fahrzeug oberhalb der Induktionsschleife (vgl. Abb. 3) befindet, so wird die Induktivität des Schwingkreises gegenüber dem Zustand ohne Fahrzeug um
verändert. Die relative Änderung
wird auch „Verstimmung“ genannt. Tab. 1 zeigt typische Verstimmungen für verschiedene Fahrzeugtypen.
Eine Veränderung der Kapazität des Kondensators im Schwingkreis ist vernachlässigbar.
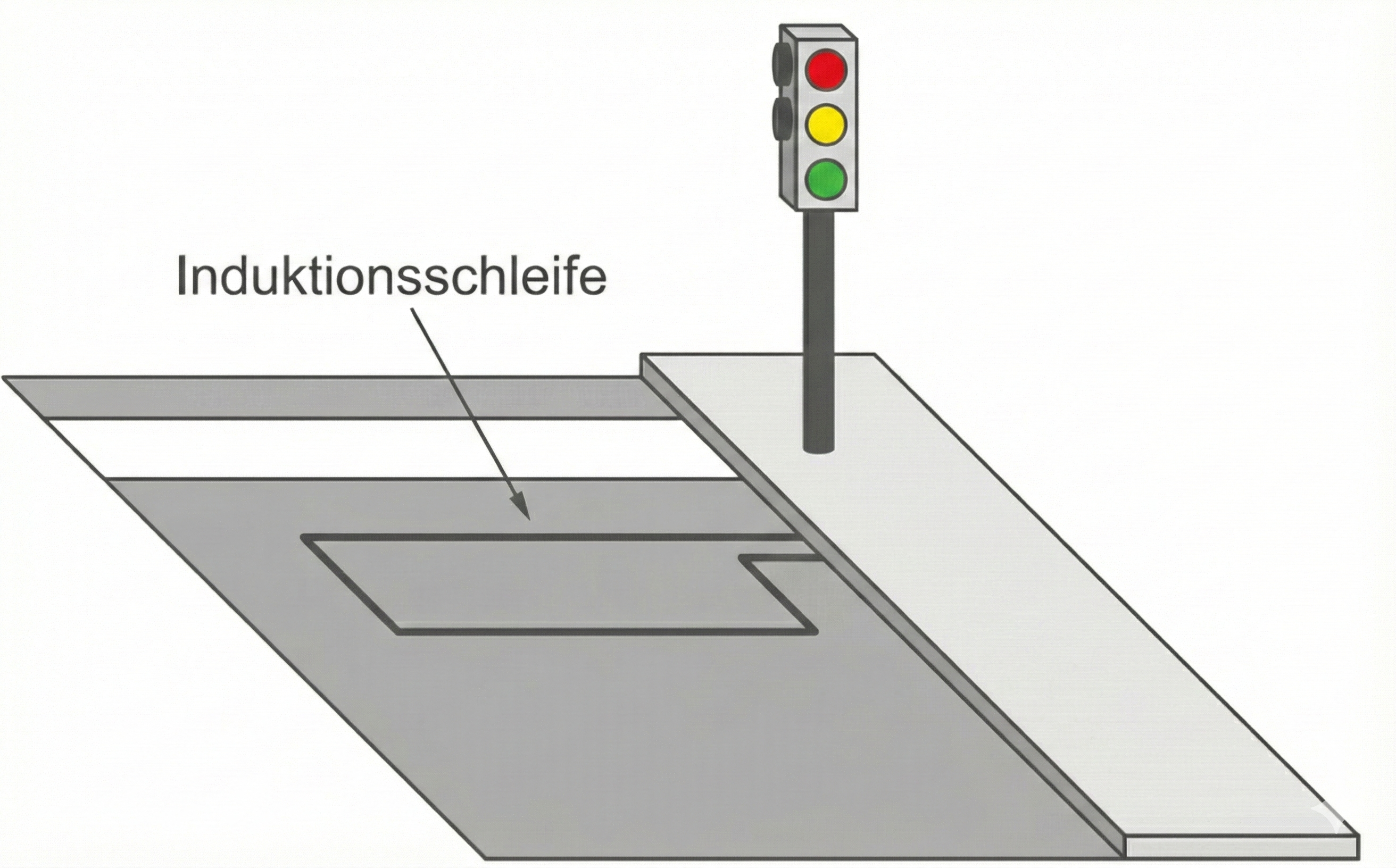
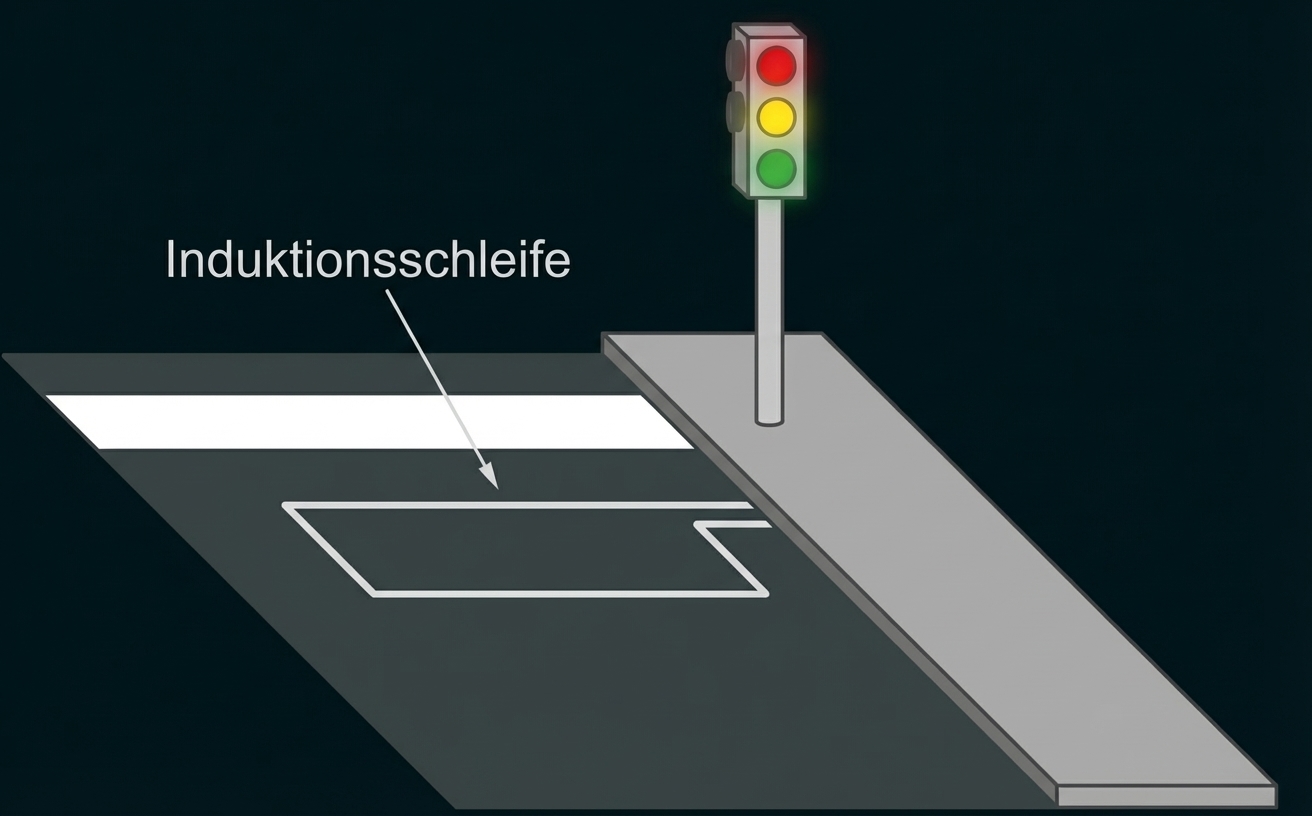
Abb. 3
|
Fahrzeugtyp |
typische Verstimmung |
|---|---|
|
PkW |
0,06 |
|
LkW |
0,015 |
|
Motorrad |
0,01 |
|
Fahrrad |
0,00018 ... 0,00022 |
Material 4: Wohin mit dem Fahrrad?
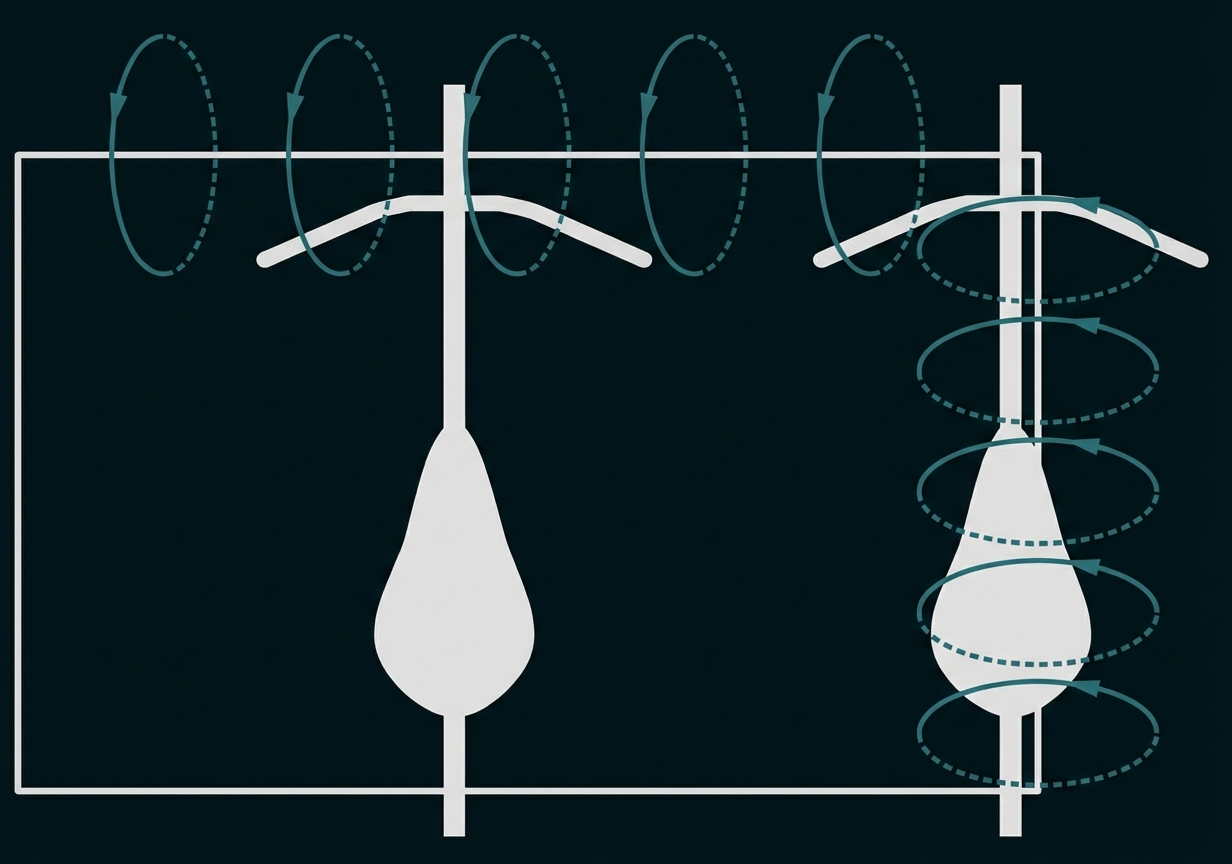
Die Schwierigkeit der Detektion eines Fahrrades liegt auch darin, dass das Magnetfeld oberhalb der Induktionsschleife nicht homogen ist und ein Fahrrad nur einen geringen Teil dieses Bereichs beeinflusst. Um eine gute Erkennung von Fahrrädern zu erreichen, sollten möglichst große Anteile des Fahrrades vom Magnetfeld des Schwingkreises durchsetzt werden, wobei die magnetische Flussdichte im Bereich des Fahrrades möglichst hoch sein sollte.
Abb. 4 zeigt zwei mögliche Positionen, die ein Fahrrad über der Induktionsschleife einnehmen kann.
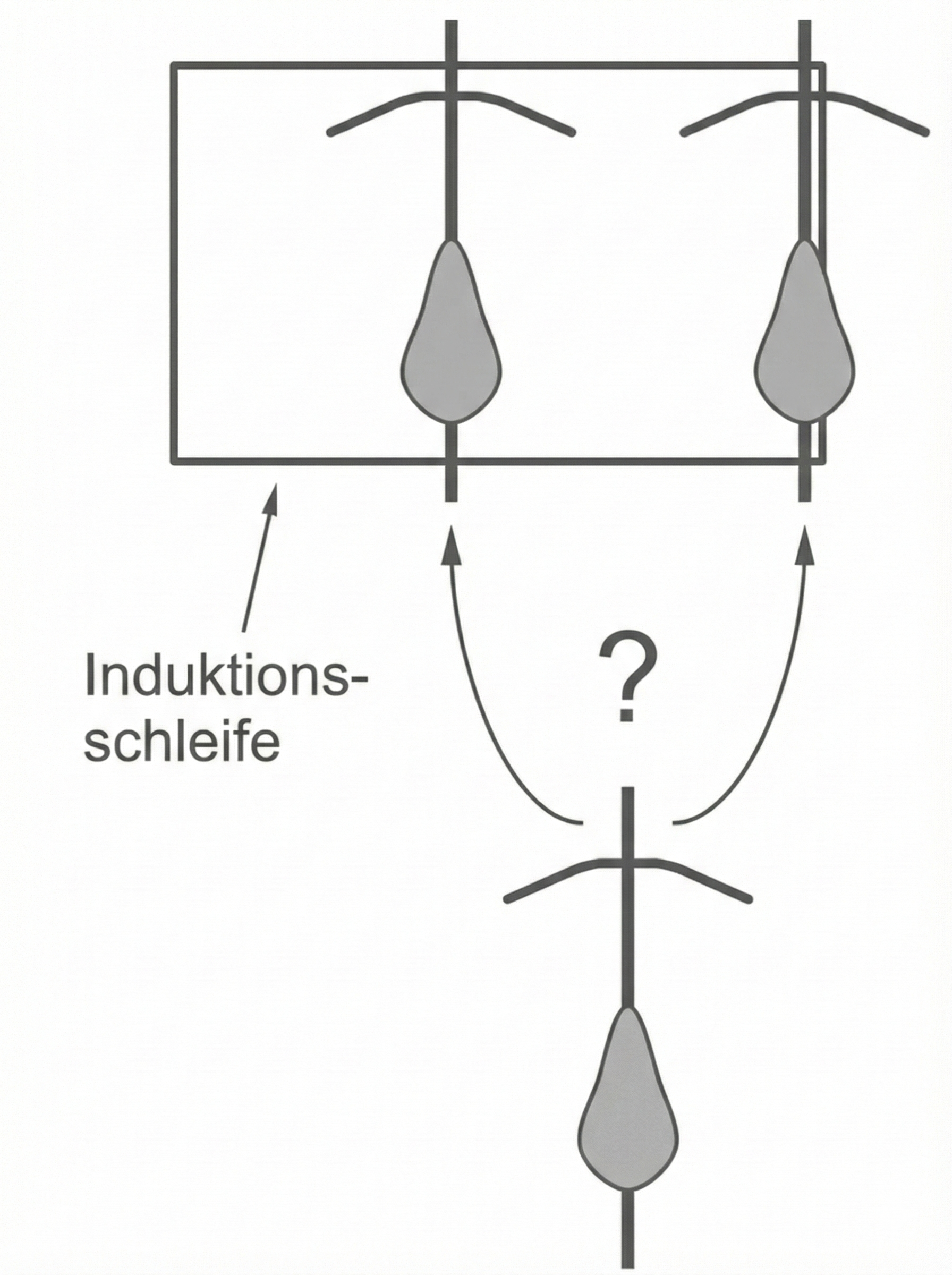
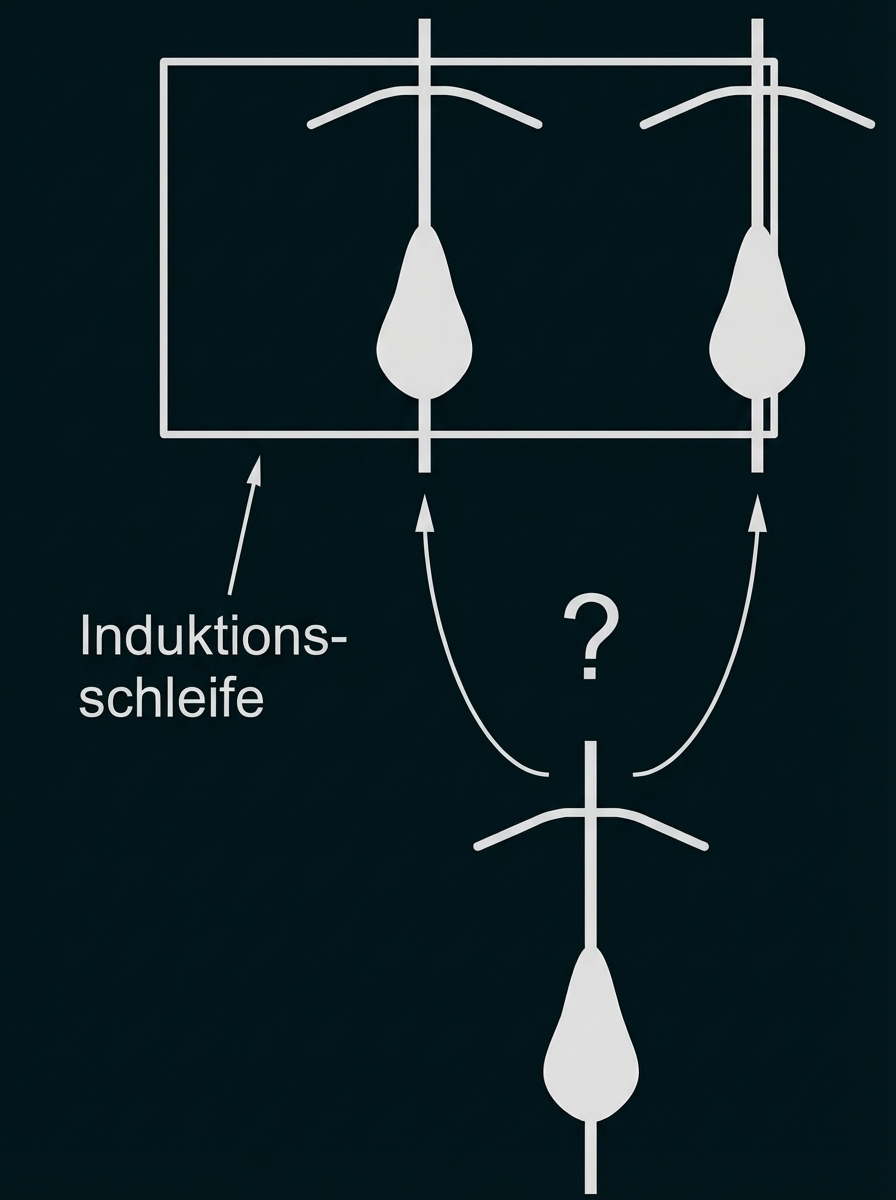
Abb. 4
Material 5: Die richtige Empfindlichkeit
Ein Hersteller von Induktionsschleifen schreibt auf seiner Homepage:
„[Statt andere Maßnahmen zu ergreifen, wird] oft versucht, durch übermäßige Erhöhung der Empfindlichkeitsstufe am Auswertgerät eine funktionierende Fahrraderfassung zu gewährleisten. Berücksichtigt man allerdings, dass auf der höchsten Empfindlichkeitsstufe eines Schleifendetektors eine Frequenzänderung von etwa 0,01 Prozent ausreicht, um ein Signal auszulösen, kann man sich vorstellen, dass diese Einstellung im Praxisbetrieb zu ständigen Störungen führt. Das Auswertgerät reagiert dabei auf kleinste Änderungen der Umgebung und neigt dazu, sich „aufzuhängen“. [Dadurch können keine Fahrzeuge mehr erfasst werden.]
Quelle: Stadlmayr Verkehrssysteme (Hrsg.): Induktionsschleifen für automatische Schranken
Verfügbar unter: https://www.stadlmayr.at/fahrradschleifen.html (Zugriff am 7.5.2023)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
Dem Materialtext entnimmt man, dass die Momentangeschwindigkeit des Pendelkörpers die analoge Größe zur momentanen Stromstärke
ist. Da
die zeitliche Änderung der Auslenkung
und
die zeitliche Änderung der Ladung auf dem Kondensator ist, lässt sich in Fortsetzung der Analogie folgern, dass die Größe „Auslenkung“ in der mechanischen Schwingung der Größe „Ladung“ in der elektromagnetischen Schwingung entspricht.
Die Frequenz des Schwingkreises ist der Kehrwert der Schwingungsdauer
kann Abb. 2 in Material 2 entnommen werden. Um den relativen Ablesefehler möglichst klein zu halten, wird die Dauer
für mehrere Perioden abgelesen und dieser Wert dann durch die Periodenanzahl
dividiert, auf diese Weise sinkt der relative Fehler auf den
-ten Wert. Für
kann aus dem Diagramm
abgelesen werden, also folgt:
Die Amplitude der abgebildeten -Kurve beträgt
Die Funktionsgleichung lautet:
Die Stromstärke besitzt bei den Wert
Die Thomson'sche Schwingungsgleichung lautet:
Durch Quadrieren und Umstellen nach und Einsetzen der Zahlenwerte ergibt sich für die Induktivität:
-
Das ferromagnetische Eisen des Fahrzeugs wird vom Magnetfeld der Induktionsschleife magnetisiert, was zu einer Erhöhung der Flussdichte in der Umgebung führt.
-
Wegen der elektrischen Leitfähigkeit des Eisens entstehen im Eisen Wirbelströme, die wiederum das Magnetfeld schwächen.
Der Tabelle kann entnommen werden, dass die Verstimmung beim Pkw 4-mal so groß ist wie die des Lkw. Eine mögliche Ursache könnte darin liegen, dass der Abstand der Bodenplatte von der Straße beim Lkw deutlich größer ist als beim tieferliegenden Pkw.
Diese Hypothese lässt sich experimentell überprüfen, indem die Verstimmung einer zur Indukionsschleifenfläche parallelen Eisenplatte in Abhängigkeit vom gegenseitigen Abstand gemessen wird.
Wenn laut der Tabelle in Material 3 die Verstimmung durch ein Fahrrad zwischen
und
liegt, dann liegt die (erhöhte) Induktivität
zwischen dem
- und dem
-fachen Wert von
Für die zugehörigen Frequenzen im Schwingkreis folgt:
Beträgt die Verstimmung der Induktivität (untere Grenze der angegebenen Tabellenwerte), dann ist die Frequenzänderung kleiner als die Empfindlichkeitsgrenze der Messvorrichtung von
und wird somit nicht erkannt.
Die magnetische Flussdichte ist in der Nähe der Leiterschleife höher als in größerer Entfernung.
Steht das Rad rechts am Rand über der Leitung, dann wird ein größerer Teil des Fahrrades vom starken Feld erfasst als bei mittiger Position des Fahrrads, wo nur Vorder- und Hinterteil des
Fahrrades im relevanten Feldbereich liegen. Folglich beeinflusst das Eisen des rechtsstehenden Fahrrads das Magnetfeld stärker als das in der Mitte stehende. Daher sollte sich die Mitschülerin rechts positionieren, um eine ausreichend große Verstimmung im Schwingkreis der Induktionsschleife hervorzurufen.
Wird die Anlage „überempfindlich“ geschaltet, reagiert sie auf irrelevante Störungen und bietet unnötige Grünphasen an, was den dann ohne Not ruhenden Querverkehr benachteiligt (erhöhter Abgasausstoß wartender Autos, Zeitverlust).
Auch der in Material 5 angesprochene drohende Geräteausfall spricht gegen die hohe Empfindlichkeit der Anlage, denn dann ist die Schutzfunktion der Anlage für den Fahrrad- und Nebenstraßenverkehr nicht gewährleistet.
Umgekehrt birgt aber auch eine zu unempfindlich geschaltete Ampelanlage Gefahren: Die Wartezeit bei Rotphasen wird für den Radverkehr bei fehlender Auslösung so groß, dass schlimmstenfalls Regelverstöße der ungeduldigen Radlerinnen oder Radler provoziert werden können, die zu Gefahrsituationen gerade für diese schwächste Verkehrsteilnehmer führen können.
Bei der Einstellung der Anlage sollten daher die genannten Grenzrisiken berücksichtigt werden und ein Mittelweg eingeschlagen werden. Um die optimale Auslösung der Induktionsschleifen zu gewährleisten, ist es zudem sinnvoll, die Radlerinnen und Radler über die richtige Positionierung an der Ampel zu informieren, am besten durch eine entsprechende Beschilderung vor Ort.